说在最前面:最近扩散模型突然很火,甚至出圈到了那些搞艺术搞绘画的圈子里去了。而且这类模型的表现确实是很惊人,不说那些打着open名义却不开源的公司,单说现在最多人用的stable diffusion,输出效果有目共睹。但是这些模型背后的原理和之前的深度学习思路都不太一样,并且原论文的数学内容又非常浓厚,令人难以下咽。所以,本篇正文内容是来自于非常详尽的推导与解释的论文“Understanding Diffusion Models: A Unified Perspective
另一篇优秀的解读博客:什么是Diffusion模型? - wrong.wang
通篇的通读翻译已经做完,但是细节部分我还在研究,内容随着继续解读和了解会有补充与更正,业内同学请随意提出订正意见以及想法交流。
引言:生成模型
给定一个样本x \boldsymbol{x} x 生成模型的目标是学习如何建立数学模型,用这个模型描述真实的数据分布p ( x ) p(\boldsymbol{x}) p ( x )
目前有几个比较常见的研究方向,本文只做一些高度概括的介绍。生成对抗网络(GAN)通过对抗学习的方法建模一个采样过程,这个采样是从一个复杂的分布中进行的。另一种“基于似然的(likelihood-based)”生成模型尝试学一个模型,让观测数据在这个模型上获得更高的似然值,包括自回归模型(autoregressive models),标准化流(normalizing flows),变分自编码器(Variational Autoencoders,VAEs)。另一种类似的方法是基于能量的(energy-based)模型,用任意的能量函数学一个分布,之后对他归一化。
基于score的生成模型和本篇主题非常相关,相比于学习如何建模能量函数,这种方法通过神经网络学到基于能量模型的得分(score)。本篇的内容研究了扩散模型,在后文中会看到,这种方法可以通过“基于似然的”也可以通过“基于得分”的视角进行解读。本文尽可能详尽地展开了扩散模型背后的数学细节,即使二年级都可以理解扩散模型以及他的工作原理。
背景知识:ELBO,VAE,Hierarchical VAE
对于许多模态,我们可以把观测到的数据当作是从一个没见过的相关的隐变量(latent variable)中生成或者表示出来的,这个隐变量可以记作随机变量z \boldsymbol{z} z 柏拉图的洞穴(Allegory of the Cave) ,讲的是,有一群人一辈子呆在一个洞穴里,他们只能看到面前洞壁上二维的影子,而这些影子是在一堆火前面的三维物体形成的。对于洞里的人而言,他们能观测到的所有东西实际上是由他们看不到的高维抽象概念决定的。
图:柏拉图的洞穴,来源Wiki百科
类似地,我们在现实世界中遇到的东西也可能是从一些高维函数产生的东西。比如说,有一些表示颜色、大小、形状,等等抽象的表示,然后这些抽象高维表示投影到了三维空间,形成了我们看到的东西,就像洞里的那些人观测到的东西实际上只是三维物体的影子。不过,洞里那些人虽说从没见过或者能理解三维物体,他们还是能思考以及推理一些阴影背后的规律。与此类似的是,我们也可以估计一些隐表示(latent representations)来描述我们观察到的数据。
尽管柏拉图的洞穴描述了这种隐变量背后的思想:隐含的观测不到的东西决定了能观测到的东西,不过这个比喻提醒了我们,在生成模型中我们通常希望学到一种低维的隐表示,而非高维的。因为在缺少很强的先验知识时,很难学习比观测维度还高维的表示。另一方面,学一个低维的隐表示同时可以看作是一种压缩,也许能发现一些对描述观测结果有语义意义的结构。
证据下界(Evidence Lower Bound,ELBO)
从数学角度出发,我们可以想象隐变量和我们观测到的数据服从一个联合分布p ( x , z ) p(\boldsymbol{x},\boldsymbol{z}) p ( x , z ) x \boldsymbol{x} x p ( x ) p(\boldsymbol{x}) p ( x ) p ( x ) p(\boldsymbol{x}) p ( x )
一种方法是边缘化 隐变量p ( z ) p(\boldsymbol{z}) p ( z ) x \boldsymbol{x} x
(1) p ( x ) = ∫ p ( x , z ) d z p(\boldsymbol{x})=\int p(\boldsymbol{x}, \boldsymbol{z}) d \boldsymbol{z} \tag {1}
p ( x ) = ∫ p ( x , z ) d z ( 1 )
或者利用概率链式法则 (根据条件概率公式推导得来):
(2) p ( x ) = p ( x , z ) p ( z ∣ x ) p(\boldsymbol{x})=\frac{p(\boldsymbol{x}, \boldsymbol{z})}{p(\boldsymbol{z}|\boldsymbol{x})} \tag {2}
p ( x ) = p ( z ∣ x ) p ( x , z ) ( 2 )
不过直接计算并且最大化似然p ( x ) p(\boldsymbol{x}) p ( x ) z \boldsymbol{z} z p ( z ∣ x ) p(\boldsymbol{z}|\boldsymbol{x}) p ( z ∣ x ) ELBO 的项,正如其名,他代表证据(evidence) 的下界。这个例子里,证据被量化为观测数据的对数似然。之后,最大化ELBO就成为了优化隐变量模型的一个间接的替代目标。在最佳的情况下,当ELBO被充分的参数化和优化到极致的时候,他就完全等同于证据。形式上,ELBO的公式写作:
(3) E q ϕ ( z ∣ x ) [ log p ( x , z ) q ϕ ( z ∣ x ) ] \mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z} | \boldsymbol{x})}\left[\log \frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\boldsymbol{\phi}}(\boldsymbol{z} | \boldsymbol{x})}\right] \tag {3}
E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p ( x , z ) ] ( 3 )
为了更清晰的展示ELBO和证据p ( x ) p(\boldsymbol{x}) p ( x )
(4) log p ( x ) ≥ E q ϕ ( z ∣ x ) [ log p ( x , z ) q ϕ ( z ∣ x ) ] \log p(\boldsymbol{x}) \geq \mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z} | \boldsymbol{x})}\left[\log \frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\boldsymbol{\phi}}(\boldsymbol{z} | \boldsymbol{x})}\right] \tag {4}
log p ( x ) ≥ E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p ( x , z ) ] ( 4 )
这里的q ϕ ( z ∣ x ) q_{\boldsymbol{\phi}}(\boldsymbol{z} | \boldsymbol{x}) q ϕ ( z ∣ x ) ϕ \boldsymbol{\phi} ϕ x \boldsymbol{x} x p ( z ∣ x ) p(\boldsymbol{z}|\boldsymbol{x}) p ( z ∣ x ) ϕ \boldsymbol{\phi} ϕ
通过公式1可以推出ELBO,过程如下:
上面的推导直接从Jensen不等式得到了一个下界,但是为什么ELBO就是证据的下界?并且只知道ELBO是数据的下界也还是无法理解为什么要把他当作目标函数进行最大化。为了更好的理解证据和ELBO之间的关系,继续用公式2来做另一个推导:
从上面推导的公式15可以很清晰的看到证据等于ELBO+KL散度(近似后验q ϕ ( z ∣ x ) q_{\boldsymbol{\phi}}(\boldsymbol{z} | \boldsymbol{x}) q ϕ ( z ∣ x ) p ( z ∣ x ) p(\boldsymbol{z} | \boldsymbol{x}) p ( z ∣ x )
第一,现在应该能理解为何ELBO是一个下界了:证据比ELBO多出来的就是一个非负的KL散度项,所以ELBO的值永远不会超过证据的值。
第二,来研究一下为什么要最大化ELBO。引入想建模的隐变量z \boldsymbol{z} z q ϕ ( z ∣ x ) q_{\boldsymbol{\phi}}(\boldsymbol{z} | \boldsymbol{x}) q ϕ ( z ∣ x ) p ( z ∣ x ) p(\boldsymbol{z} | \boldsymbol{x}) p ( z ∣ x ) p ( z ∣ x ) p(\boldsymbol{z} | \boldsymbol{x}) p ( z ∣ x ) log p ( x ) \log p(\boldsymbol{x}) log p ( x ) ϕ \boldsymbol{\phi} ϕ p ( x ∣ z ) p(\boldsymbol{x} | \boldsymbol{z}) p ( x ∣ z ) z \boldsymbol{z} z ϕ \boldsymbol{\phi} ϕ ϕ \boldsymbol{\phi} ϕ log p ( x ) \log p(\boldsymbol{x}) log p ( x )
变分自编码器(Variational Autoencoders,VAE)
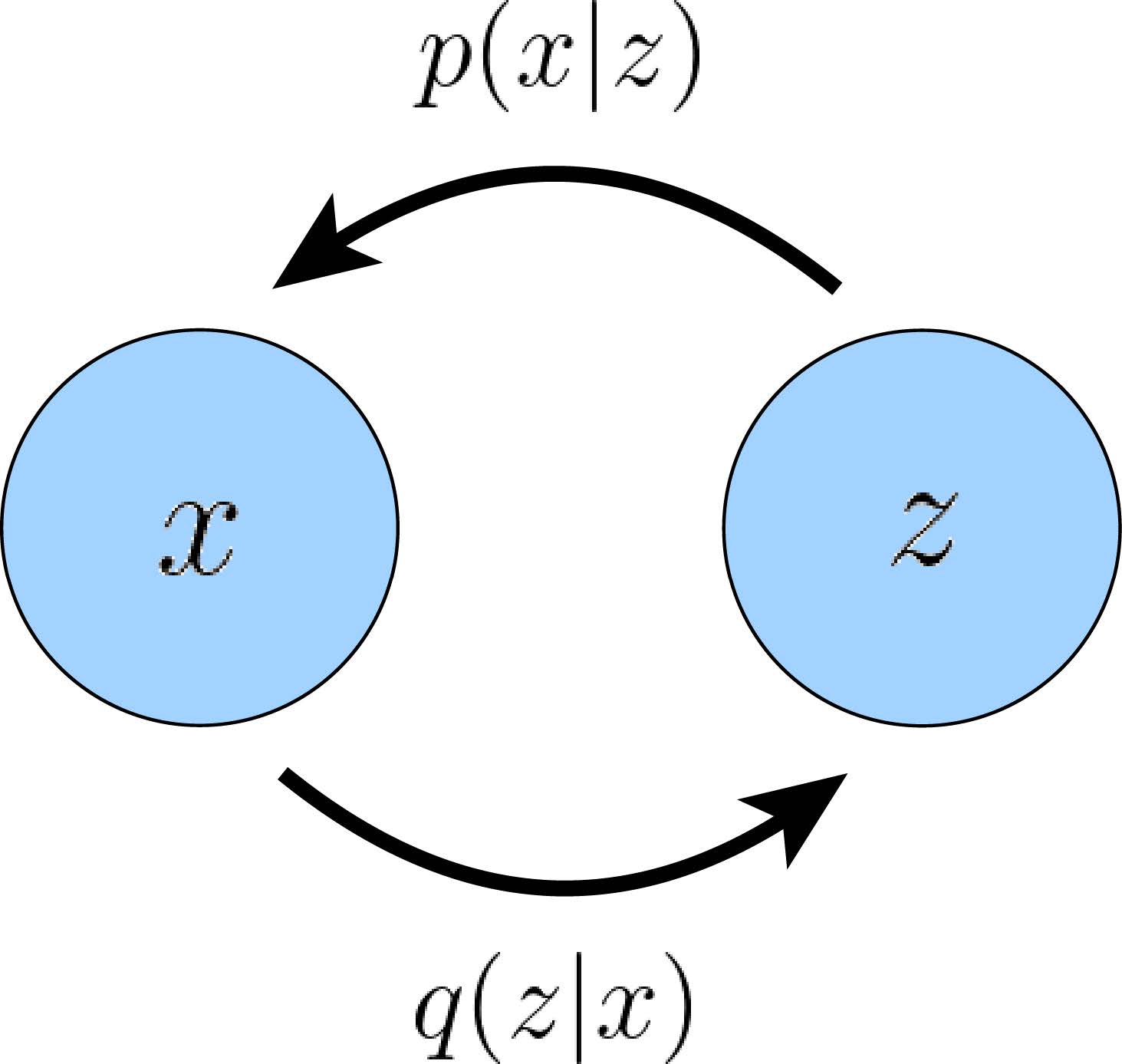
图1:VAE的图示。其中,编码器q ( z ∣ x ) q(\boldsymbol{z}|\boldsymbol{x}) q ( z ∣ x ) x \boldsymbol{x} x z \boldsymbol{z} z p ( x ∣ z ) p(\boldsymbol{x}|\boldsymbol{z}) p ( x ∣ z )
在VAE原始论文里面[1 ]直接最大化ELBO,这个方法是变分的(variational),因为我们要在一群参数为ϕ \boldsymbol{\phi} ϕ q ϕ ( z ∣ x ) q_{\boldsymbol{\phi}}(\boldsymbol{z} | \boldsymbol{x}) q ϕ ( z ∣ x ) 自编码器(autoencoder)这个名字的由来和传统的自动编码模型有关系,这种模型输入数据后,经过一些中间层,再输出这个数据本身。为了清楚的看到一些关联,下面再仔细研究一下ELBO项:
在这里,需要学习一个可以被视作是编码器(encoder)的中间分布q ϕ ( z ∣ x ) q_{\boldsymbol{\phi}}(\boldsymbol{z} | \boldsymbol{x}) q ϕ ( z ∣ x ) p θ ( x ∣ z ) p_{\boldsymbol{\theta}}(\boldsymbol{x} | \boldsymbol{z}) p θ ( x ∣ z ) z \boldsymbol{z} z x \boldsymbol{x} x 解码器(decoder)。
公式19里面的两项都有直观解释:第一项从变分分布衡量解码器的重建似然,确保学到的分布能够有效建模隐分布,从而确保原始数据能重新生成。第二项衡量了学到的变分分布与隐变量的先验信念(prior belief)之间有多像,最小化这一项能够促使编码器真正学到分布,而非塌缩到Dirac delta函数上【防止模式崩溃】。最大化ELBO等同于最大化第一项,最小化第二项。
VAE的一个关键特征在于,如何在参数ϕ \boldsymbol{\phi} ϕ θ \boldsymbol{\theta} θ
(20) q ϕ ( z ∣ x ) = N ( z ; μ ϕ ( x ) , σ ϕ 2 ( x ) I ) q_\boldsymbol{\phi}(\boldsymbol{z} | \boldsymbol{x}) =\mathcal{N}\left(\boldsymbol{z} ; \boldsymbol{\mu}_\boldsymbol{\phi}(\boldsymbol{x}), \boldsymbol{\sigma}_\boldsymbol{\phi}^2(\boldsymbol{x}) \mathbf{I}\right) \tag{20}
q ϕ ( z ∣ x ) = N ( z ; μ ϕ ( x ) , σ ϕ 2 ( x ) I ) ( 2 0 )
(21) p ( z ) = N ( z ; 0 , I ) p(\boldsymbol{z}) = \mathcal{N}(\boldsymbol{z} ; \boldsymbol{0} , \mathbf{I})\tag{21}
p ( z ) = N ( z ; 0 , I ) ( 2 1 )
然后ELBO的KL散度项可以解析求得,公式19里面那个reconstruction项可以用蒙特卡洛估计法近似出来。由此目标函数可以写成:
对数据集内任意的观测值x \boldsymbol{x} x { z ( l ) } l = 1 L \left\{\boldsymbol{z}^{(l)}\right\}_{l=1}^L { z ( l ) } l = 1 L q ϕ ( z ∣ x ) q_\boldsymbol{\phi}(\boldsymbol{z}|\boldsymbol{x}) q ϕ ( z ∣ x ) z ( l ) \boldsymbol{z}^{(l)} z ( l ) q ϕ ( z ∣ x ) q_\boldsymbol{\phi}(\boldsymbol{z} | \boldsymbol{x}) q ϕ ( z ∣ x ) 重参数化 (reparameterization )的技巧来解决。
重参数化将一个随机变量表达成一个关于噪声变量的确定性的函数,这样可以对非随机项使用梯度下降法进行优化。比如说,从一个均值为μ \mu μ σ 2 \sigma^2 σ 2 x ∼ N ( x ; μ , σ 2 ) x \sim \mathcal{N}(x ; \mu, \sigma^2) x ∼ N ( x ; μ , σ 2 )
x = μ + σ ϵ with ϵ ∼ N ( ϵ ; 0 , I ) x=\mu+\sigma \epsilon \quad \text { with } \epsilon \sim \mathcal{N}(\epsilon ; 0, \mathrm{I})
x = μ + σ ϵ with ϵ ∼ N ( ϵ ; 0 , I )
也就是说,任意的高斯分布都可以转换成均值从0用加法移到μ \mu μ σ 2 \sigma^2 σ 2 ϵ \epsilon ϵ
在VAE里,每个z \boldsymbol{z} z x \boldsymbol{x} x ϵ \boldsymbol{\epsilon} ϵ
z = μ ϕ ( x ) + σ ϕ ( x ) ⊙ ϵ with ϵ ∼ N ( ϵ ; 0 , I ) \boldsymbol{z}=\boldsymbol{\mu}_\boldsymbol{\phi}(\boldsymbol{x})+\boldsymbol{\sigma}_\boldsymbol{\phi}(\boldsymbol{x}) \odot \boldsymbol{\epsilon} \quad \text { with } \boldsymbol{\epsilon} \sim \mathcal{N}(\boldsymbol{\epsilon} ; \mathbf{0}, \mathbf{I})
z = μ ϕ ( x ) + σ ϕ ( x ) ⊙ ϵ with ϵ ∼ N ( ϵ ; 0 , I )
其中⊙ \odot ⊙ z \boldsymbol{z} z ϕ \boldsymbol{\phi} ϕ μ ϕ \boldsymbol{\mu}_\boldsymbol{\phi} μ ϕ σ ϕ \boldsymbol{\sigma}_\boldsymbol{\phi} σ ϕ ϕ \boldsymbol{\phi} ϕ θ \boldsymbol{\theta} θ
训练完VAE之后,想要生成新的数据,就可以直接从隐空间p ( z ) p(\boldsymbol{z}) p ( z ) z \boldsymbol{z} z x \boldsymbol{x} x
层次化的变分自编码器(Hierarchical Variational Autoencoders,HVAE)
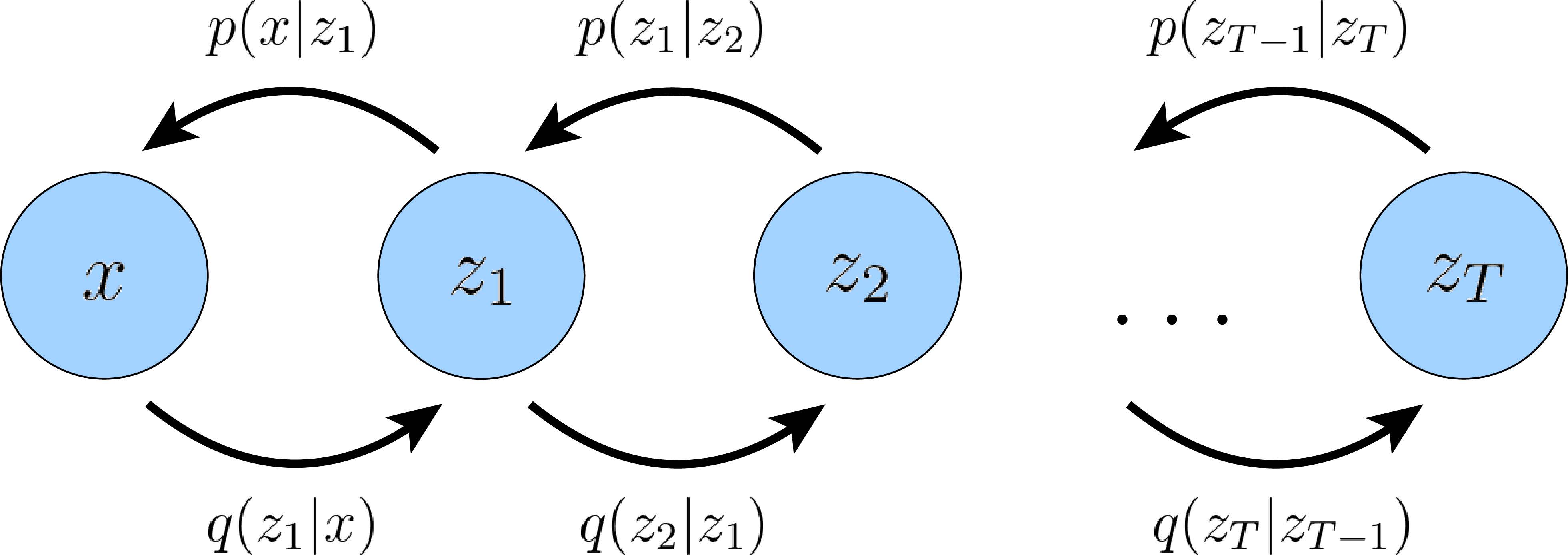
图2:有T T T z t \boldsymbol{z}_t z t z t + 1 \boldsymbol{z}_{t+1} z t + 1
HVAE[2 , 3 ]是VAE的一个推广形式,他将隐变量扩展到了多个层级,模型里的隐变量本身又是从更高级更抽象的隐变量中生成的。直觉上说,柏拉图洞穴里那些人把三维物体当作是生成二维影子的隐变量,就像是我们把更高级的抽象东西当作生成我们观测到的三维物体的隐变量。所以,在柏拉图洞穴里面的人可以把他们的观测情况建模成一个有两层(或者更多层)隐层次的过程(理解为,高级抽象->产生三维物体->产生二维影子)。
对于有T T T z t \boldsymbol{z}_t z t z t + 1 \boldsymbol{z}_{t+1} z t + 1
之后,ELBO很容易扩展一下:
把联合分布(公式23)和后验(公式24)替换到公式28里面:
下文会阐述,当我们研究变分扩散模型时,这个目标函数会进一步分解为可解释的成分。
变分扩散模型(Variational Diffusion Model,VDM)
研究VDM[4 , 5 , 6 ]的一个最简单的方法是把他看作一个MHVAE,但是有3个关键的限定条件:
隐变量维度严格等于数据维度
每个时间步的隐编码器的结构不是学到的,是一个预定义好的线性高斯模型。换句话说,是一个关于前一个时间步的输出的高斯分布
隐编码器的高斯分布参数随着时间步而改变,让最后一个时间步T T T
而且还要保持着像MHVAE那种层级之间转移的马尔可夫性。
接下来进一步阐述这些假设的含义。
从第一项约束看,我们可以把真实样本和隐变量一起表示为x t \boldsymbol{x}_t x t t = 0 t=0 t = 0 t ∈ [ 1 , T ] t \in [1, T] t ∈ [ 1 , T ] t t t
(30) q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) q\left(\boldsymbol{x}_{1: T} | \boldsymbol{x}_0\right)=\prod_{t=1}^T q\left(\boldsymbol{x}_t | \boldsymbol{x}_{t-1}\right) \tag{30}
q ( x 1 : T ∣ x 0 ) = t = 1 ∏ T q ( x t ∣ x t − 1 ) ( 3 0 )
第二项假设,我们已知编码器里的每个隐变量的分布是有关前一层隐变量的高斯分布。与MHVAE不同,每个时间步t t t 5 ],或者作为参数学到的[6 ]。用均值为μ t ( x t ) = α t x t − 1 \boldsymbol{\mu}_t(\boldsymbol{x}_t)=\sqrt{\alpha_t} \boldsymbol{x}_{t-1} μ t ( x t ) = α t x t − 1 Σ t ( x t ) = ( 1 − α t ) I \boldsymbol{\Sigma}_t(\boldsymbol{x}_t)=(1-\alpha_t) \mathbf{I} Σ t ( x t ) = ( 1 − α t ) I 保持方差 (variance-preserving )的。注意:交替进行高斯参数化也是可以的,并且能得到类似的推导。主要的结论是,α t \alpha_t α t t t t
(31) q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) q(\boldsymbol{x}_t | \boldsymbol{x}_{t-1})=\mathcal{N}\left(\boldsymbol{x}_t ; \sqrt{\alpha_t} \boldsymbol{x}_{t-1},(1-\alpha_t) \mathbf{I}\right) \tag{31}
q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) ( 3 1 )
第三项假设,可以看到α t \alpha_t α t p ( x T ) p(\boldsymbol{x}_T) p ( x T )
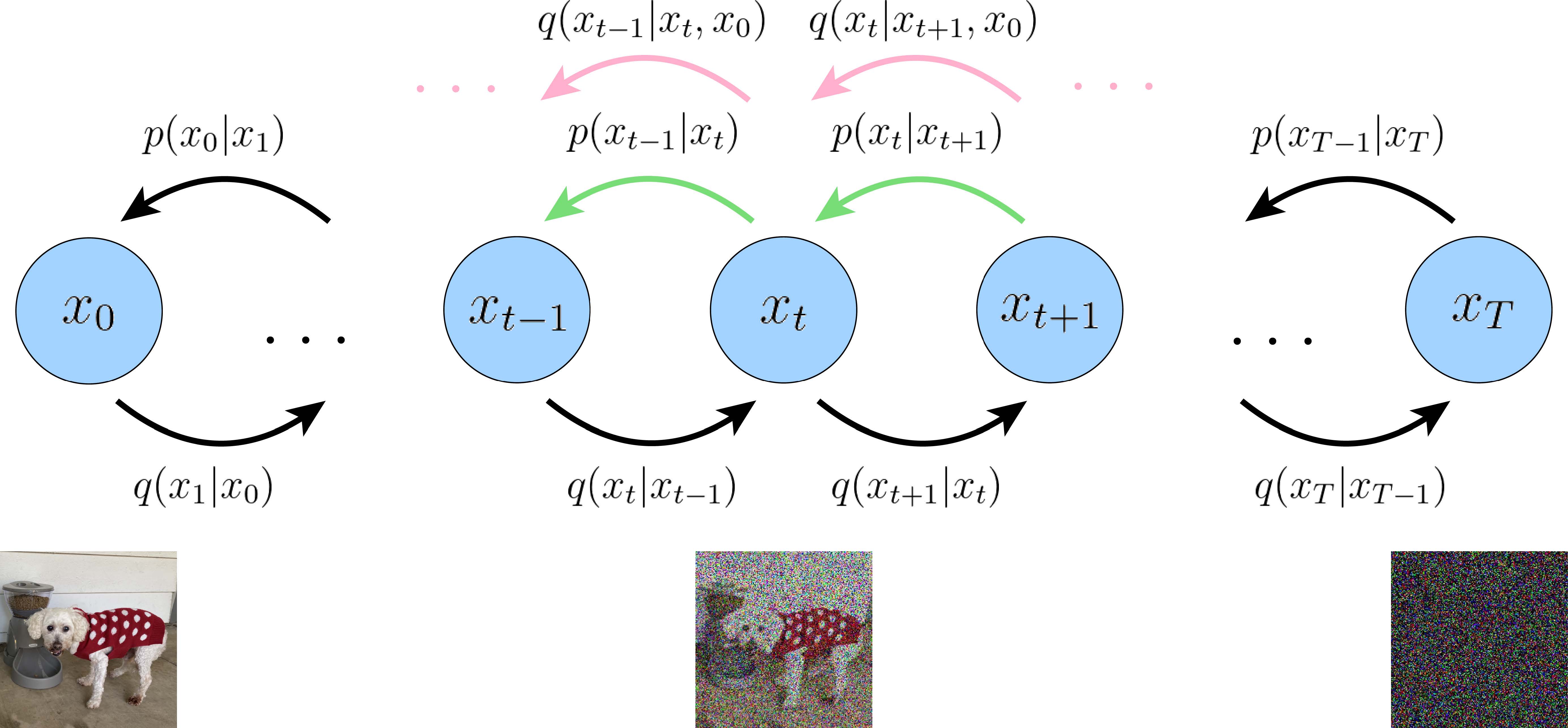
总的来说,这组假设描述了输入图像随时间的稳定加噪过程,通过添加高斯噪声来逐渐破坏图像,直到完全变成纯高斯噪声。该过程如图3所示。
图3:VDM的示意图。x 0 \boldsymbol{x}_0 x 0 x T \boldsymbol{x}_T x T x t \boldsymbol{x}_t x t x 0 \boldsymbol{x}_0 x 0 q ( x t ∣ x t − 1 ) q(\boldsymbol{x}_t|\boldsymbol{x}_{t-1}) q ( x t ∣ x t − 1 )
需要注意这里的编码器分布q ( x t ∣ x t − 1 ) q(\boldsymbol{x}_t|\boldsymbol{x}_{t-1}) q ( x t ∣ x t − 1 ) ϕ \boldsymbol{\phi} ϕ p θ ( x t − 1 ∣ x t ) p_\boldsymbol{\theta}(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) p θ ( x t − 1 ∣ x t ) p ( x T ) p(\boldsymbol{x}_T) p ( x T ) p θ ( x t − 1 ∣ x t ) p_\boldsymbol{\theta}(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) p θ ( x t − 1 ∣ x t ) T T T x 0 \boldsymbol{x}_0 x 0
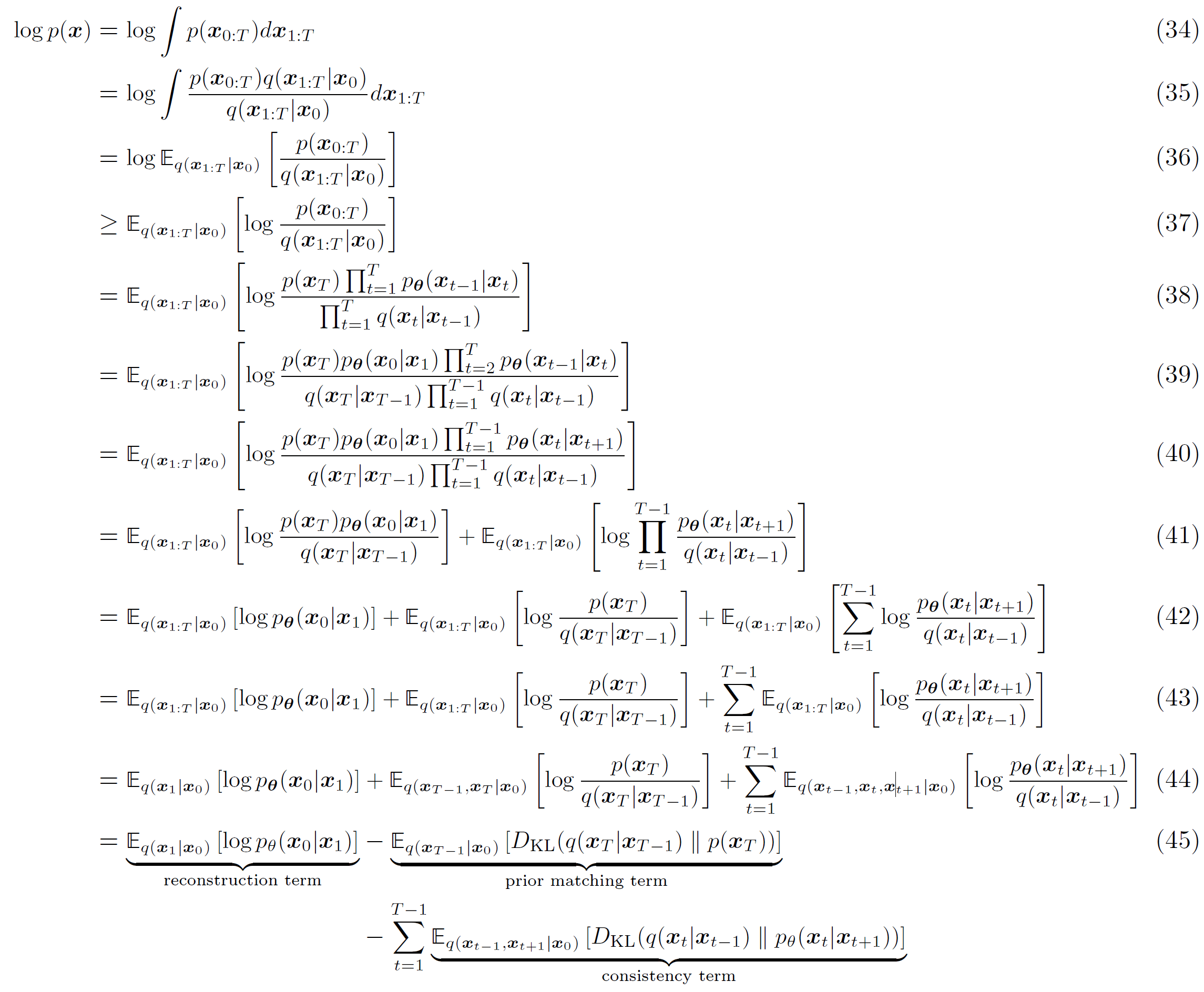
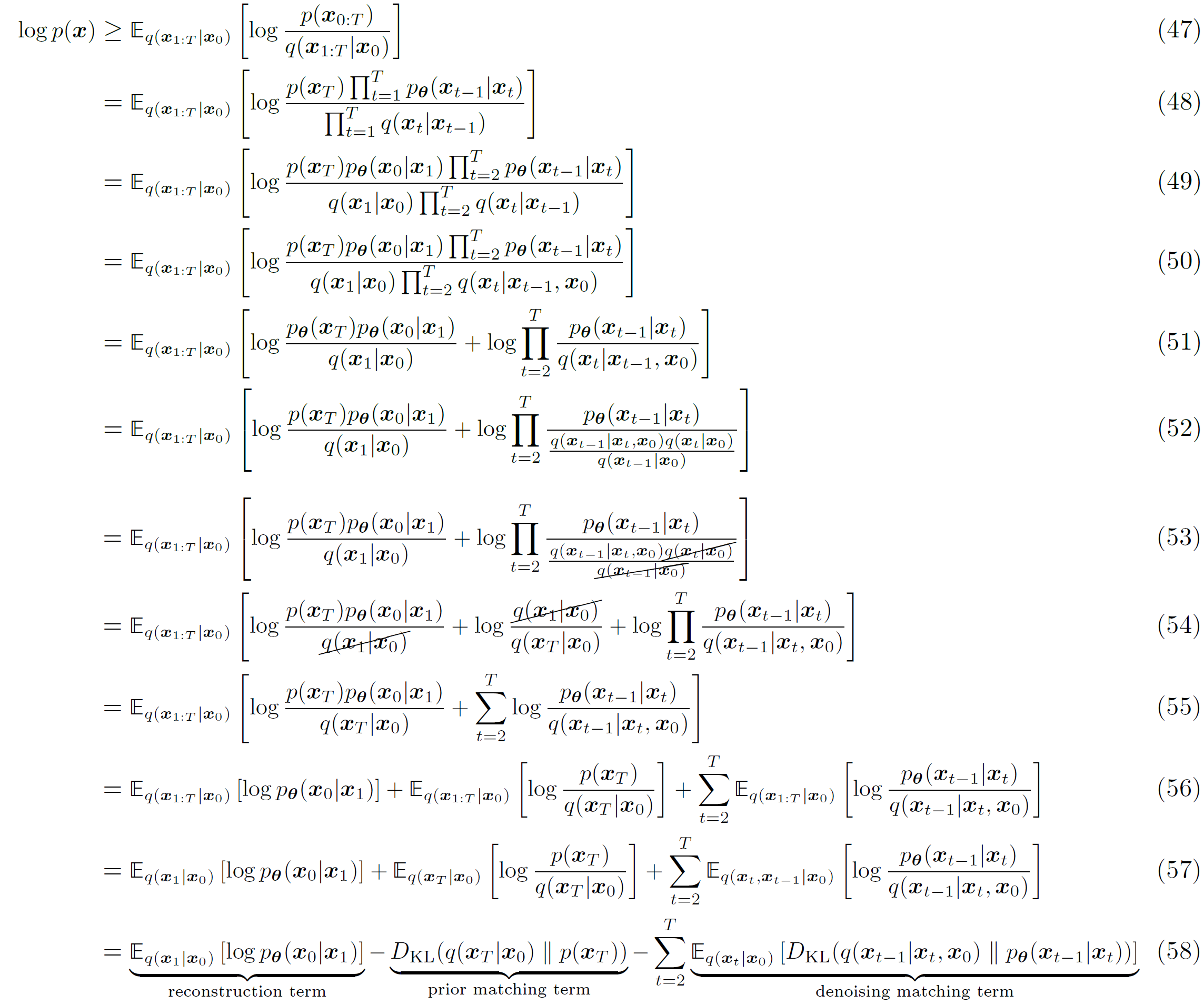
就像众多HVAE一样,VDM也可以通过最大化ELBO优化,具体推导如下:
这个形式的ELBO的每个部分有如下的解释:
E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] \mathbb{E}_{q\left(\boldsymbol{x}_1 | \boldsymbol{x}_0\right)}\left[\log p_{\boldsymbol{\theta}}(\boldsymbol{x}_0 | \boldsymbol{x}_1)\right] E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] 重建项 (reconstruction term ),用来预测给定第一步的隐变量下原始样本的对数概率。这一项也在原版VAE里面出现过,都可以用类似的办法训练。E q ( x T − 1 ∣ x 0 ) [ D K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ) ] \mathbb{E}_{q(\boldsymbol{x}_{T-1} | \boldsymbol{x}_0)}\left[D_{\mathrm{KL}}\left(q(\boldsymbol{x}_T | \boldsymbol{x}_{T-1}) \| p(\boldsymbol{x}_T)\right)\right] E q ( x T − 1 ∣ x 0 ) [ D K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ) ] 先验匹配项 (prior matching term ),在最终的隐分布和高斯先验匹配的时候最小。这一项没有可学习的参数,不需要优化。并且我们假设了一个足够大的T T T E q ( x t − 1 , x t + 1 ∣ x 0 ) [ D K L ( q ( x t ∣ x t − 1 ) ∥ p θ ( x t ∣ x t + 1 ) ) ] \mathbb{E}_{q(\boldsymbol{x}_{t-1}, \boldsymbol{x}_{t+1} | \boldsymbol{x}_0)}\left[D_{\mathrm{KL}}\left(q(\boldsymbol{x}_t | \boldsymbol{x}_{t-1}) \| p_{\boldsymbol{\theta}}(\boldsymbol{x}_t | \boldsymbol{x}_{t+1})\right)\right] E q ( x t − 1 , x t + 1 ∣ x 0 ) [ D K L ( q ( x t ∣ x t − 1 ) ∥ p θ ( x t ∣ x t + 1 ) ) ] 一致项 (consistency term ),让x t \boldsymbol{x}_t x t p θ ( x t ∣ x t + 1 ) p_{\boldsymbol{\theta}}(\boldsymbol{x}_t | \boldsymbol{x}_{t+1}) p θ ( x t ∣ x t + 1 ) q ( x t ∣ x t − 1 ) q(\boldsymbol{x}_t | \boldsymbol{x}_{t-1}) q ( x t ∣ x t − 1 )
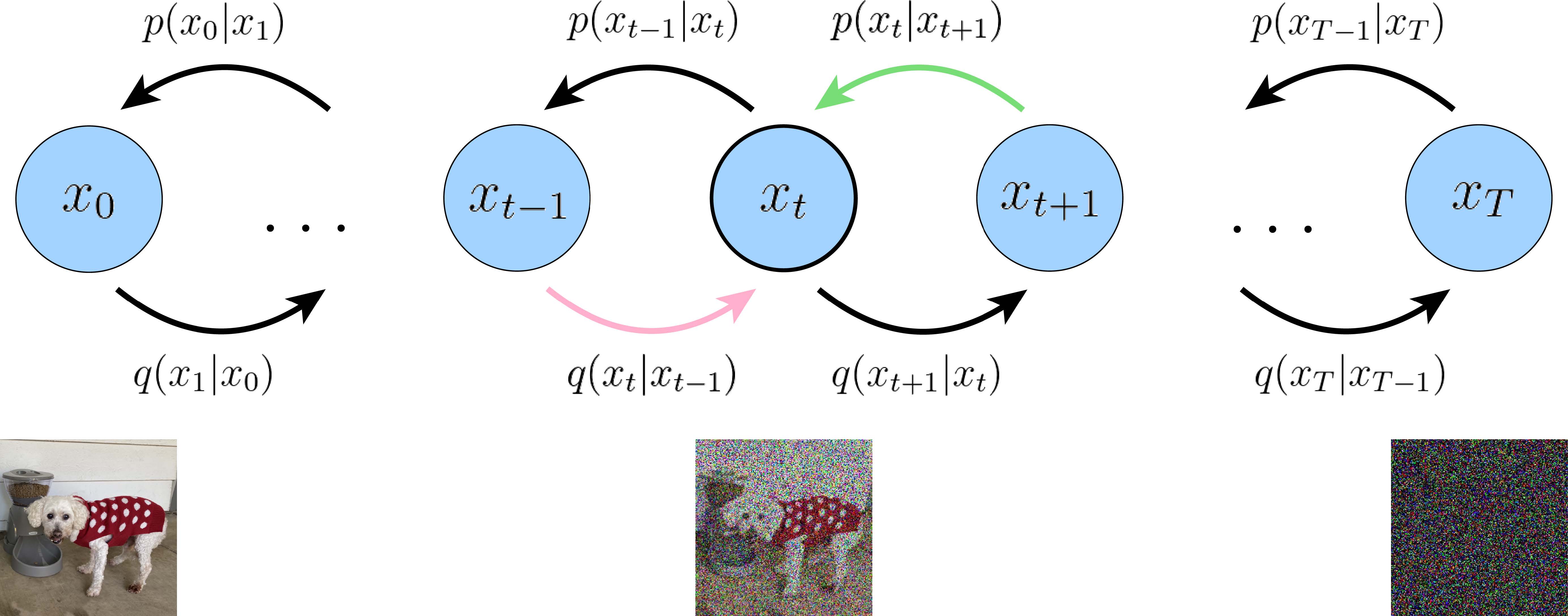
直观来看,这个关于ELBO的解释如图4所示。优化VDM的成本开销主要在第三项上,因为必须在所有时间步t t t
图4:在第一个推导里面,对于每一个中间的x t \boldsymbol{x}_t x t p θ ( x t ∣ x t + 1 ) p_{\boldsymbol{\theta}}(\boldsymbol{x}_t | \boldsymbol{x}_{t+1}) p θ ( x t ∣ x t + 1 ) q ( x t ∣ x t − 1 ) q(\boldsymbol{x}_t | \boldsymbol{x}_{t-1}) q ( x t ∣ x t − 1 ) x t \boldsymbol{x}_t x t
在这个推导下,ELBO的所有项都用期望计算,因此可以使用蒙特卡洛估计进行近似。但是直接用我们刚刚推导出来的东西去优化ELBO并不是最优的,因为一致项在每个时间步下是两个随机变量的期望{ x t − 1 , x t + 1 } \{\boldsymbol{x}_{t-1}, \boldsymbol{x}_{t+1}\} { x t − 1 , x t + 1 } T T T T − 1 T-1 T − 1
接下来尝试让每个期望都只和一个随机变量相关,再推导一下ELBO。一个重要的想法是,编码器的转移可以重写成q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 ) q(\boldsymbol{x}_t | \boldsymbol{x}_{t-1})=q(\boldsymbol{x}_t | \boldsymbol{x}_{t-1}, \boldsymbol{x}_0) q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 )
(46) q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) q(\boldsymbol{x}_t | \boldsymbol{x}_{t-1}, \boldsymbol{x}_0)=\frac{q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t, \boldsymbol{x}_0) q(\boldsymbol{x}_t | \boldsymbol{x}_0)}{q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_0)} \tag{46}
q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x 0 ) q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) ( 4 6 )
有了这个新式子以后,可以尝试重新从公式37开始,写一下ELBO的推导过程:
由此我们就推出了一个估算方差更小的ELBO,其中每个时间步的每一项都是最多一个随机变量的期望。这个表达中的每一项也有很好的解释:
E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] \mathbb{E}_{q\left(\boldsymbol{x}_1 | \boldsymbol{x}_0\right)}\left[\log p_{\boldsymbol{\theta}}(\boldsymbol{x}_0 | \boldsymbol{x}_1)\right] E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] D K L ( q ( x T ∣ x 0 ) ∥ p ( x T ) ) D_{\mathrm{KL}}(q(\boldsymbol{x}_T | \boldsymbol{x}_{0}) \| p(\boldsymbol{x}_T)) D K L ( q ( x T ∣ x 0 ) ∥ p ( x T ) ) E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ] \mathbb{E}_{q(\boldsymbol{x}_{t} | \boldsymbol{x}_0)}\left[D_{\mathrm{KL}}\left(q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t}, \boldsymbol{x}_{0} ) \| p_{\boldsymbol{\theta}}(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t})\right)\right] E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ] 去噪匹配项 (denoising matching term )。我们想要得到的去噪转移p θ ( x t − 1 ∣ x t ) p_{\boldsymbol{\theta}}(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t}) p θ ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x t , x 0 ) q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t}, \boldsymbol{x}_{0}) q ( x t − 1 ∣ x t , x 0 ) q ( x t − 1 ∣ x t , x 0 ) q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t}, \boldsymbol{x}_{0}) q ( x t − 1 ∣ x t , x 0 ) x 0 \boldsymbol{x}_{0} x 0 x t \boldsymbol{x}_{t} x t
在两个ELBO推导过程(公式45和公式58)中,只用到了马尔可夫假设。因此,这些公式适用于任意的MHVAE。此外,当T = 1 T=1 T = 1
在这个ELBO的推导过程中,优化成本大部分花在了求和项也就是重建项(不应该是去噪匹配项吗?)上面。而由于同时学习编码器导致复杂度增加,每一个KL散度项D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) D_{\mathrm{KL}}\left(q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t}, \boldsymbol{x}_{0} ) \| p_{\boldsymbol{\theta}}(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t})\right) D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) )
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) q\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t, \boldsymbol{x}_0\right)=\frac{q\left(\boldsymbol{x}_t | \boldsymbol{x}_{t-1}, \boldsymbol{x}_0\right) q\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_0\right)}{q\left(\boldsymbol{x}_t | \boldsymbol{x}_0\right)}
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x 0 ) q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 )
从编码器转移的假设(公式31)可以知道q ( x t ∣ x t − 1 , x 0 ) = q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) q\left(\boldsymbol{x}_t | \boldsymbol{x}_{t-1}, \boldsymbol{x}_0\right)=q\left(\boldsymbol{x}_t | \boldsymbol{x}_{t-1}\right)=\mathcal{N}\left(\boldsymbol{x}_t ; \sqrt{\alpha_t} \boldsymbol{x}_{t-1},\left(1-\alpha_t\right) \mathbf{I}\right) q ( x t ∣ x t − 1 , x 0 ) = q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) q ( x t ∣ x 0 ) q(\boldsymbol{x}_t | \boldsymbol{x}_{0}) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{0}) q ( x t − 1 ∣ x 0 ) x t ∼ q ( x t ∣ x t − 1 ) \boldsymbol{x}_t \sim q(\boldsymbol{x}_t | \boldsymbol{x}_{t-1}) x t ∼ q ( x t ∣ x t − 1 )
(59) x t = α t x t − 1 + 1 − α t ϵ with ϵ ∼ N ( ϵ ; 0 , I ) \boldsymbol{x}_t=\sqrt{\alpha_t} \boldsymbol{x}_{t-1}+\sqrt{1-\alpha_t} \boldsymbol{\epsilon} \quad \text { with } \boldsymbol{\epsilon} \sim \mathcal{N}(\boldsymbol{\epsilon} ; \mathbf{0}, \mathbf{I}) \tag{59}
x t = α t x t − 1 + 1 − α t ϵ with ϵ ∼ N ( ϵ ; 0 , I ) ( 5 9 )
与之类似,从x t − 1 ∼ q ( x t − 1 ∣ x t − 2 ) \boldsymbol{x}_{t-1} \sim q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t-2}) x t − 1 ∼ q ( x t − 1 ∣ x t − 2 )
(60) x t − 1 = α t − 1 x t − 2 + 1 − α t − 1 ϵ with ϵ ∼ N ( ϵ ; 0 , I ) \boldsymbol{x}_{t-1}=\sqrt{\alpha_{t-1}} \boldsymbol{x}_{t-2}+\sqrt{1-\alpha_{t-1}} \boldsymbol{\epsilon} \quad \text { with } \boldsymbol{\epsilon} \sim \mathcal{N}(\boldsymbol{\epsilon} ; \mathbf{0}, \mathbf{I}) \tag{60}
x t − 1 = α t − 1 x t − 2 + 1 − α t − 1 ϵ with ϵ ∼ N ( ϵ ; 0 , I ) ( 6 0 )
之后,q ( x t ∣ x 0 ) q(\boldsymbol{x}_{t} | \boldsymbol{x}_{0}) q ( x t ∣ x 0 ) 2 T 2T 2 T { ϵ t ∗ , ϵ t } t = 0 T ∼ i i d N ( ϵ ; 0 , I ) \left\{\boldsymbol{\epsilon}_t^*, \boldsymbol{\epsilon}_t\right\}_{t=0}^T \stackrel{\mathrm{iid}}{\sim} \mathcal{N}(\boldsymbol{\epsilon} ; \mathbf{0}, \mathbf{I}) { ϵ t ∗ , ϵ t } t = 0 T ∼ i i d N ( ϵ ; 0 , I ) x t ∼ q ( x t ∣ x 0 ) \boldsymbol{x}_t \sim q(\boldsymbol{x}_t | \boldsymbol{x}_{0}) x t ∼ q ( x t ∣ x 0 )
在公式64里面应用了独立随机高斯变量求和 的方法,即均值相加,方差相加。将1 − α t ϵ t − 1 ∗ \sqrt{1-\alpha_t} \boldsymbol{\epsilon}_{t-1}^* 1 − α t ϵ t − 1 ∗ N ( 0 , ( 1 − α t ) I ) \mathcal{N}(\mathbf{0},(1-\alpha_t) \mathbf{I}) N ( 0 , ( 1 − α t ) I ) α t − α t α t − 1 ϵ t − 2 ∗ \sqrt{\alpha_t-\alpha_t\alpha_{t-1}} \boldsymbol{\epsilon}_{t-2}^* α t − α t α t − 1 ϵ t − 2 ∗ N ( 0 , ( α t − α t α t − 1 ) I ) \mathcal{N}(\mathbf{0},(\alpha_t-\alpha_t\alpha_{t-1}) \mathbf{I}) N ( 0 , ( α t − α t α t − 1 ) I ) N ( 0 , ( 1 − α t + α t − α t α t − 1 ) I ) = N ( 0 , ( 1 − α t α t − 1 ) I ) \mathcal{N}(\mathbf{0},(1-\alpha_t+\alpha_t-\alpha_t \alpha_{t-1}) \mathbf{I})=\mathcal{N}(\mathbf{0},(1-\alpha_t \alpha_{t-1}) \mathbf{I}) N ( 0 , ( 1 − α t + α t − α t α t − 1 ) I ) = N ( 0 , ( 1 − α t α t − 1 ) I ) 1 − α t α t − 1 ϵ t − 2 \sqrt{1-\alpha_t\alpha_{t-1}} \boldsymbol{\epsilon}_{t-2} 1 − α t α t − 1 ϵ t − 2
图5:一个低方差的优化VDM的替代方案。根据贝叶斯公式计算真实的去噪的形式q ( x t − 1 ∣ x t , x 0 ) q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t}, \boldsymbol{x}_{0}) q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) p_\boldsymbol{\theta}(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t}) p θ ( x t − 1 ∣ x t ) x 0 \boldsymbol{x}_{0} x 0
由此便获得了q ( x t ∣ x 0 ) q(\boldsymbol{x}_{t} | \boldsymbol{x}_{0}) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{0}) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) q(\boldsymbol{x}_{t} | \boldsymbol{x}_{0}) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{0}) q ( x t − 1 ∣ x 0 ) q ( x t − 1 ∣ x t , x 0 ) q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t}, \boldsymbol{x}_{0}) q ( x t − 1 ∣ x t , x 0 )
在公式75里,C ( x t , x 0 ) C(\boldsymbol{x}_{t}, \boldsymbol{x}_{0}) C ( x t , x 0 ) x t , x 0 , α \boldsymbol{x}_{t}, \boldsymbol{x}_{0}, \alpha x t , x 0 , α x t − 1 \boldsymbol{x}_{t-1} x t − 1
由此可以看到,对于每一步,x t − 1 ∼ q ( x t − 1 ∣ x t , x 0 ) \boldsymbol{x}_{t-1} \sim q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t, \boldsymbol{x}_0) x t − 1 ∼ q ( x t − 1 ∣ x t , x 0 ) μ q ( x t , x 0 ) \boldsymbol{\mu}_q(\boldsymbol{x}_t, \boldsymbol{x}_0) μ q ( x t , x 0 ) x t \boldsymbol{x}_t x t x 0 \boldsymbol{x}_0 x 0 Σ q ( t ) \boldsymbol{\Sigma}_q(t) Σ q ( t ) α \alpha α α \alpha α Σ q ( t ) = σ q 2 ( t ) I \boldsymbol{\Sigma}_q(t)=\sigma_q^2(t) \mathbf{I} Σ q ( t ) = σ q 2 ( t ) I
(85) σ q 2 ( t ) = ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t \sigma_q^2(t)=\frac{\left(1-\alpha_t\right)\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \tag{85}
σ q 2 ( t ) = 1 − α ˉ t ( 1 − α t ) ( 1 − α ˉ t − 1 ) ( 8 5 )
为了尽量匹配近似的去噪转移步骤p θ ( x t − 1 ∣ x t ) p_{\boldsymbol{\theta}}(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t) p θ ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x t , x 0 ) q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t, \boldsymbol{x}_0) q ( x t − 1 ∣ x t , x 0 ) α \alpha α Σ q ( t ) = σ q 2 ( t ) I \boldsymbol{\Sigma}_q(t)=\sigma_q^2(t) \mathbf{I} Σ q ( t ) = σ q 2 ( t ) I p θ ( x t − 1 ∣ x t ) p_{\boldsymbol{\theta}}(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t) p θ ( x t − 1 ∣ x t ) x 0 \boldsymbol{x}_0 x 0 μ θ ( x t , t ) \boldsymbol{\mu}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right) μ θ ( x t , t ) x t \boldsymbol{x}_t x t
回忆一下,两个高斯分布的KL散度 是
当我们设置两个高斯分布的方差让他俩尽可能匹配,优化KL散度项即为最小化两个分布的均值的差距:
这里μ q \boldsymbol{\mu}_q μ q μ q ( x t , x 0 ) \boldsymbol{\mu}_q(\boldsymbol{x}_t, \boldsymbol{x}_0) μ q ( x t , x 0 ) μ θ \boldsymbol{\mu}_\boldsymbol{\theta} μ θ μ θ ( x t , t ) \boldsymbol{\mu}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) μ θ ( x t , t ) μ θ ( x t , t ) \boldsymbol{\mu}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) μ θ ( x t , t ) μ q ( x t , x 0 ) \boldsymbol{\mu}_q(\boldsymbol{x}_t, \boldsymbol{x}_0) μ q ( x t , x 0 )
(93) μ q ( x t , x 0 ) = α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x 0 1 − α ˉ t \boldsymbol{\mu}_q\left(\boldsymbol{x}_t, \boldsymbol{x}_0\right)=\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right) \boldsymbol{x}_t+\sqrt{\bar{\alpha}_{t-1}}\left(1-\alpha_t\right) \boldsymbol{x}_0}{1-\bar{\alpha}_t} \tag{93}
μ q ( x t , x 0 ) = 1 − α ˉ t α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x 0 ( 9 3 )
因为μ θ ( x t , t ) \boldsymbol{\mu}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) μ θ ( x t , t ) x t \boldsymbol{x}_t x t μ q ( x t , x 0 ) \boldsymbol{\mu}_q(\boldsymbol{x}_t, \boldsymbol{x}_0) μ q ( x t , x 0 )
(94) μ θ ( x t , t ) = α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x ^ θ ( x t , t ) 1 − α ˉ t \boldsymbol{\mu}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)=\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right) \boldsymbol{x}_t+\sqrt{\bar{\alpha}_{t-1}}\left(1-\alpha_t\right) \hat{\boldsymbol{x}}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)}{1-\bar{\alpha}_t} \tag{94}
μ θ ( x t , t ) = 1 − α ˉ t α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x ^ θ ( x t , t ) ( 9 4 )
其中x ^ θ ( x t , t ) \hat{\boldsymbol{x}}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) x ^ θ ( x t , t ) x t \boldsymbol{x}_t x t t t t x 0 \boldsymbol{x}_0 x 0
因此,优化VDM成为了训练一个神经网络从任意的带噪图像预测原始的真实图像的问题[5 ]。并且最小化之前推导出的ELBO(公式58)的各个噪音级别上的求和项也可以通过最小化所有时间步的期望的方法近似,并且可以通过在时间步上随机采样进行优化:
(100) arg min θ E t ∼ U { 2 , T } [ E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ] ] \underset{\boldsymbol{\theta}}{\arg \min } \mathbb{E}_{t \sim U\{2, T\}}\left[\mathbb{E}_{q\left(\boldsymbol{x}_t | \boldsymbol{x}_0\right)}\left[D_{\mathrm{KL}}\left(q\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t, \boldsymbol{x}_0\right) \| p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t\right)\right)\right]\right] \tag{100}
θ arg min E t ∼ U { 2 , T } [ E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ] ] ( 1 0 0 )
学习扩散噪声参数
下面看一下VDM的噪声参数是如何联合学习的。一种可行的方法是使用一个参数为η \boldsymbol{\eta} η α ^ η ( t ) \hat{\alpha}_{\boldsymbol{\eta}}(t) α ^ η ( t ) α t {\alpha}_t α t t t t α ˉ t \bar{\alpha}_t α ˉ t
看公式70,q ( x t ∣ x 0 ) q\left(\boldsymbol{x}_t | \boldsymbol{x}_0\right) q ( x t ∣ x 0 ) N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) \mathcal{N}\left(\boldsymbol{x}_t ; \sqrt{\bar{\alpha}_t} \boldsymbol{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right) N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) 信噪比 的定义,S N R = μ 2 σ 2 \mathrm{SNR}=\frac{\mu^2}{\sigma^2} S N R = σ 2 μ 2 t t t
(109) SNR ( t ) = α ˉ t 1 − α ˉ t \operatorname{SNR}(t)=\frac{\bar{\alpha}_t}{1-\bar{\alpha}_t} \tag{109}
S N R ( t ) = 1 − α ˉ t α ˉ t ( 1 0 9 )
之后,公式108(和公式99)可以简化为:
正如其名,信噪比表示的是原始信号和所包含噪声的比例,信噪比高代表信号更强,低代表噪声更强。在扩散模型里面,我们需要信噪比随着时间步t t t x t \boldsymbol{x}_t x t t = T t=T t = T
简化公式110的目标之后,我们可以直接在每个时间步用一个神经网络参数化信噪比,并且和扩散模型一起联合学习。因为信噪比是随时间单调递减的,可以表示为:
(111) SNR ( t ) = exp ( − ω η ( t ) ) \operatorname{SNR}(t)=\exp \left(-\omega_{\boldsymbol{\eta}}(t)\right) \tag{111}
S N R ( t ) = exp ( − ω η ( t ) ) ( 1 1 1 )
这里ω η ( t ) \omega_{\boldsymbol{\eta}}(t) ω η ( t ) η \boldsymbol{\eta} η η \boldsymbol{\eta} η α ˉ t \bar{\alpha}_t α ˉ t 1 − α ˉ t 1-\bar{\alpha}_t 1 − α ˉ t
这些项在各种计算中都有用,例如在优化时,他们可以用来通过重参数化从输入x 0 \boldsymbol{x}_0 x 0 x t \boldsymbol{x}_t x t
三个等价表示
在前面的证明中,VDM可以通过简单的训练一个神经网络来预测原始的自然图像x 0 \boldsymbol{x}_0 x 0 x t \boldsymbol{x}_t x t t t t x 0 \boldsymbol{x}_0 x 0
首先,利用重参数化技巧,在对于q ( x t ∣ x 0 ) q(\boldsymbol{x}_t | \boldsymbol{x}_0) q ( x t ∣ x 0 )
(115) x 0 = x t − 1 − α ˉ t ϵ 0 α ˉ t \boldsymbol{x}_0=\frac{\boldsymbol{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_0}{\sqrt{\bar{\alpha}_t}} \tag{115}
x 0 = α ˉ t x t − 1 − α ˉ t ϵ 0 ( 1 1 5 )
代入到前面推导的真实去噪转移均值μ q ( x t , x 0 ) \boldsymbol{\mu}_q(\boldsymbol{x}_t, \boldsymbol{x}_0) μ q ( x t , x 0 )
由此,近似去噪转移均值μ θ ( x t , t ) \boldsymbol{\mu}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) μ θ ( x t , t )
(125) μ θ ( x t , t ) = 1 α t x t − 1 − α t 1 − α ˉ t α t ϵ ^ θ ( x t , t ) \boldsymbol{\mu}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)=\frac{1}{\sqrt{\alpha_t}} \boldsymbol{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t} \sqrt{\alpha_t}} \hat{\boldsymbol{\epsilon}}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right) \tag{125}
μ θ ( x t , t ) = α t 1 x t − 1 − α ˉ t α t 1 − α t ϵ ^ θ ( x t , t ) ( 1 2 5 )
以及对应的优化问题(公式95)变成:
这里,ϵ ^ θ ( x t , t ) \hat{\boldsymbol{\epsilon}}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) ϵ ^ θ ( x t , t ) ϵ 0 ∼ N ( ϵ ; 0 , I ) \epsilon_0 \sim \mathcal{N}(\boldsymbol{\epsilon} ; \mathbf{0}, \mathbf{I}) ϵ 0 ∼ N ( ϵ ; 0 , I ) x 0 \boldsymbol{x}_0 x 0 x t \boldsymbol{x}_t x t x 0 \boldsymbol{x}_0 x 0 5 , 7 ]发现预测噪声的性能更好。
为了推导第三种常见的VDM的表示,要引入Tweedie公式[8 ],Tweedie公式表示,给定从指数族分布中抽取的样本,这个分布的真实平均值可以通过样本的最大似然估计值(又称经验平均值)加上与估计分数有关的一些修正项来估计。对于只有一个观测样本的情况,经验平均值只是样本本身。如果观测样本都位于某个分布的一端,则负分数变大,并将样本的朴素最大似然估计值往真实平均值修正,用于减轻样本偏差。
从数学上来说,对于一个高斯变量z ∼ N ( z ; μ z , Σ z ) z \sim \mathcal{N}(z ; \boldsymbol{\mu}_z, \boldsymbol{\Sigma}_z) z ∼ N ( z ; μ z , Σ z )
E [ μ z ∣ z ] = z + Σ z ∇ z log p ( z ) \mathbb{E}[\boldsymbol{\mu}_z | \boldsymbol{z}]=\boldsymbol{z}+\boldsymbol{\Sigma}_z \nabla_{\boldsymbol{z}} \log p(\boldsymbol{z})
E [ μ z ∣ z ] = z + Σ z ∇ z log p ( z )
在这里,我们用它来预测给定样本x t \boldsymbol{x}_t x t
q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) q\left(\boldsymbol{x}_t | \boldsymbol{x}_0\right)=\mathcal{N}\left(\boldsymbol{x}_t ; \sqrt{\bar{\alpha}_t} \boldsymbol{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right)
q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I )
然后使用Tweedie公式:
(131) E [ μ x t ∣ x t ] = x t + ( 1 − α ˉ t ) ∇ x t log p ( x t ) \mathbb{E}[\boldsymbol{\mu}_{x_t} | \boldsymbol{x}_t]=\boldsymbol{x}_t+\left(1-\bar{\alpha}_t\right) \nabla_{\boldsymbol{x}_t} \log p\left(\boldsymbol{x}_t\right) \tag{131}
E [ μ x t ∣ x t ] = x t + ( 1 − α ˉ t ) ∇ x t log p ( x t ) ( 1 3 1 )
这里∇ x t log p ( x t ) \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{x}_t) ∇ x t log p ( x t ) ∇ log p ( x t ) \nabla \log p(\boldsymbol{x}_t) ∇ log p ( x t ) x t \boldsymbol{x}_t x t μ x t = α ˉ t x 0 \boldsymbol{\mu}_{x_t}=\sqrt{\bar{\alpha}_t} \boldsymbol{x}_0 μ x t = α ˉ t x 0
之后可以将公式133代入真实的去噪转移均值μ q ( x t , x 0 ) \boldsymbol{\mu}_q(\boldsymbol{x}_t, \boldsymbol{x}_0) μ q ( x t , x 0 )
由此可以把近似去噪转移均值μ θ ( x t , t ) \boldsymbol{\mu}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) μ θ ( x t , t )
(143) μ θ ( x t , t ) = 1 α t x t + 1 − α t α t s θ ( x t , t ) \boldsymbol{\mu}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)=\frac{1}{\sqrt{\alpha_t}} \boldsymbol{x}_t+\frac{1-\alpha_t}{\sqrt{\alpha_t}} \boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right) \tag{143}
μ θ ( x t , t ) = α t 1 x t + α t 1 − α t s θ ( x t , t ) ( 1 4 3 )
以及对应的优化问题:
这里的s θ ( x t , t ) \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) s θ ( x t , t ) ∇ x t log p ( x t ) \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{x}_t) ∇ x t log p ( x t ) x t \boldsymbol{x}_t x t
细心的读者应该已经发现得分函数∇ log p ( x t ) \nabla \log p(\boldsymbol{x}_t) ∇ log p ( x t ) ϵ 0 \boldsymbol{\epsilon}_0 ϵ 0
事实证明,这两项之间仅仅差一个随时间变化的常数因子!得分函数衡量如何在数据空间内移动来最大化对数概率,直观地说,由于源噪声被添加到自然图像中以扰乱图像,因此朝相反方向移动会对图像进行“去噪”,这是提升后续对数概率的最佳更新。我们的数学证明也证实了这个直觉,已经明确表明,学习对得分函数建模等同于对源噪声的负值建模(相差一个比例因子)。
至此我们推出了三种等价的优化VDM的目标:学习一个神经网络来预测(1)原始图像x 0 \boldsymbol{x}_0 x 0 ϵ 0 \boldsymbol{\epsilon}_0 ϵ 0 ∇ log p ( x t ) \nabla \log p(\boldsymbol{x}_t) ∇ log p ( x t ) t t t
基于得分的(Score-based)生成模型
前面展示了VDM可以通过简单的优化一个神经网络s θ ( x t , t ) \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) s θ ( x t , t ) ∇ log p ( x t ) \nabla \log p(\boldsymbol{x}_t) ∇ log p ( x t ) 9 , 10 , 11 ]。事实上,我们可以证明,我们之前推导的VDM和基于得分的生成模型公式之间等价,这样就可以灵活切换这两种解释。
为了开始理解为什么优化得分函数是有意义的,我们绕道而行,重新访问基于能量的模型[12 , 13 ],任意可变的概率分布可以写成
(152) p θ ( x ) = 1 Z θ e − f θ ( x ) p_{\boldsymbol{\theta}}(\boldsymbol{x})=\frac{1}{Z_{\boldsymbol{\theta}}} e^{-f_{\boldsymbol{\theta}}(\boldsymbol{x})} \tag{152}
p θ ( x ) = Z θ 1 e − f θ ( x ) ( 1 5 2 )
这里f θ ( x ) f_{\boldsymbol{\theta}}(\boldsymbol{x}) f θ ( x ) Z_{\boldsymbol{\theta} 是一个归一化常数,用来确保∫ p θ ( x ) d x = 1 \int p_{\boldsymbol{\theta}}(\boldsymbol{x}) d \boldsymbol{x}=1 ∫ p θ ( x ) d x = 1 Z θ = ∫ e − f θ ( x ) d x Z_{\boldsymbol{\theta}}=\int e^{-f_{\boldsymbol{\theta}}(\boldsymbol{x})} d \boldsymbol{x} Z θ = ∫ e − f θ ( x ) d x f θ ( x ) f_{\boldsymbol{\theta}}(\boldsymbol{x}) f θ ( x )
一种避免计算或者建模这个归一化常数的方法是使用神经网络s θ ( x ) \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}) s θ ( x ) ∇ log p ( x ) \nabla \log p(\boldsymbol{x}) ∇ log p ( x ) p ( x ) p(\boldsymbol{x}) p ( x )
这样可以在不涉及任何归一化常数的情况下利用神经网络表示。得分模型可以通过最小化与真实得分函数的Fisher Divergence优化:
(157) E p ( x ) [ ∥ s θ ( x ) − ∇ log p ( x ) ∥ 2 2 ] \mathbb{E}_{p(\boldsymbol{x})}\left[\left\|s_{\boldsymbol{\theta}}(\boldsymbol{x})-\nabla \log p(\boldsymbol{x})\right\|_2^2\right] \tag{157}
E p ( x ) [ ∥ s θ ( x ) − ∇ log p ( x ) ∥ 2 2 ] ( 1 5 7 )
图6:用朗之万动力学生成的三个随机采样轨迹的可视化,所有这些轨迹都从同一初始点开始,用于高斯混合。左图在三维轮廓上绘制这些采样轨迹,而右图根据真实的得分函数绘制采样轨迹。由于朗之万动力学采样过程中的随机噪声项,我们能够从相同的初始点从不同的模式生成样本。如果没有噪声,每次试验从一个固定的点进行抽样总是会遵循固定的得分,最终到达相同的模式。
得分函数代表了什么?对于任意x \boldsymbol{x} x x \boldsymbol{x} x x \boldsymbol{x} x
(158) x i + 1 ← x i + c ∇ log p ( x i ) + 2 c ϵ , i = 0 , 1 , … , K \boldsymbol{x}_{i+1} \leftarrow \boldsymbol{x}_i+c \nabla \log p\left(\boldsymbol{x}_i\right)+\sqrt{2 c} \boldsymbol{\epsilon}, \quad i=0,1, \ldots, K \tag{158}
x i + 1 ← x i + c ∇ log p ( x i ) + 2 c ϵ , i = 0 , 1 , … , K ( 1 5 8 )
其中x 0 \boldsymbol{x}_0 x 0
注意公式157的目标依赖于真实的得分函数,但这在复杂分布(例如对自然图像的建模)中是不可用的。好在其他的技术,称之为得分匹配(score matching)[14 , 15 , 16 , 17 ]被用于最小化这个Fisher divergence而不必知道真实的得分,同时它可以利用随机梯度下降方法做优化。
总的来说,学习将分布表示为一个得分函数,并使用马尔可夫链蒙特卡罗(MCMC)技术生成样本(如朗之万动力学),被称为基于得分的生成模型[9 , 10 , 11 ]。
正如Song和Ermon[9 ]所详述的那样,原版的得分匹配存在三个主要问题。
首先,当x \boldsymbol{x} x
第二,在低密度区域,通过原版的得分匹配训练到的得分函数不准确,从我们在公式157中最小化的目标可以明显看出这一点。因为它是对p ( x ) p(\boldsymbol{x}) p ( x )
最后,郎之万动力学采样可能不会混合,即使使用真实得分进行采样。假设真实数据分布是两个不相交分布的混合:
(159) p ( x ) = c 1 p 1 ( x ) + c 2 p 2 ( x ) p(\boldsymbol{x})=c_1 p_1(\boldsymbol{x})+c_2 p_2(\boldsymbol{x}) \tag{159}
p ( x ) = c 1 p 1 ( x ) + c 2 p 2 ( x ) ( 1 5 9 )
之后,当计算得分时,这些混合系数会消失,因为对数运算将系数从分布中分离出来,梯度运算将其归零。为了可视化这一点,请注意图6的右图,真实的得分函数不知道三种分布之间的不同权重。尽管右下角的那个模式在实际的高斯混合中具有更高的权重,但从这个初始化点进行的朗之万动力学采样到达每个模式的机会大致相等。
事实证明,通过向数据中添加多级高斯噪声,可以同时解决这三个缺点。首先,由于高斯噪声分布的支持(support)是整个空间,受扰动的数据样本将不再局限于低维流形。其次,加入较大的高斯噪声将增加每个模式在数据分布中覆盖的面积,在低密度区域增加更多的训练信号。最后,添加多级方差增加的高斯噪声将带来与真实的混合系数相关的中间分布。
形式上,我们可以选择正的噪声级别序列{ σ t } t = 1 T \left\{\sigma_t\right\}_{t=1}^T { σ t } t = 1 T
(160) p σ t ( x t ) = ∫ p ( x ) N ( x t ; x , σ t 2 I ) d x p_{\sigma_t}\left(\boldsymbol{x}_t\right)=\int p(\boldsymbol{x}) \mathcal{N}\left(\boldsymbol{x}_t ; \boldsymbol{x}, \sigma_t^2 \mathbf{I}\right) d \boldsymbol{x} \tag{160}
p σ t ( x t ) = ∫ p ( x ) N ( x t ; x , σ t 2 I ) d x ( 1 6 0 )
之后,训练一个神经网络,通过得分匹配来同时在所有噪声级别上学习得分函数:
(161) arg min θ ∑ t = 1 T λ ( t ) E p σ t ( x t ) [ ∥ s θ ( x , t ) − ∇ log p σ t ( x t ) ∥ 2 2 ] \underset{\boldsymbol{\theta}}{\arg \min } \sum_{t=1}^T \lambda(t) \mathbb{E}_{p_{\sigma_t}\left(\boldsymbol{x}_t\right)}\left[\left\|\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}, t)-\nabla \log p_{\sigma_t}\left(\boldsymbol{x}_t\right)\right\|_2^2\right] \tag{161}
θ arg min t = 1 ∑ T λ ( t ) E p σ t ( x t ) [ ∥ s θ ( x , t ) − ∇ log p σ t ( x t ) ∥ 2 2 ] ( 1 6 1 )
其中λ ( t ) \lambda(t) λ ( t ) t t t t = T , T − 1 , . . . , 2 , 1 t=T,T-1,...,2,1 t = T , T − 1 , . . . , 2 , 1 t t t
至此,我们在VDM和基于得分的生成模型的训练目标和抽样过程中建立了明确的联系。
一个问题是,如何自然地将扩散模型推广到无限的时间步数。在MHVAE的视角下,这可以解释为将层次的数量扩展到无穷T → ∞ T \rightarrow \infty T → ∞ 10 ]。不同的SDE参数化过程本质上描述了不同的随时间变化的扰动方案,从而实现了加噪过程的灵活建模[6 ]。
引导
到现在我们一置关注着对数据分布p ( x ) p(\boldsymbol{x}) p ( x ) p ( x ∣ y ) p(\boldsymbol{x}|y) p ( x ∣ y ) y y y 18 ])和目前最前沿的图像文本模型(DALL-E 2 [19 ], Imagen [7 ])。
一种自然的想法是,要想加入条件信息,就把他加在每轮的时间步信息上。回想一下公式32的联合分布:
p ( x 0 : T ) = p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) p\left(\boldsymbol{x}_{0: T}\right)=p\left(\boldsymbol{x}_T\right) \prod_{t=1}^T p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)
p ( x 0 : T ) = p ( x T ) t = 1 ∏ T p θ ( x t − 1 ∣ x t )
然后,为了把这个转换成条件扩散模型,可以简单的加入任意条件信息y y y
(162) p ( x 0 : T ∣ y ) = p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t , y ) p\left(\boldsymbol{x}_{0: T} \mid y\right)=p\left(\boldsymbol{x}_T\right) \prod_{t=1}^T p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, y\right) \tag{162}
p ( x 0 : T ∣ y ) = p ( x T ) t = 1 ∏ T p θ ( x t − 1 ∣ x t , y ) ( 1 6 2 )
举例来说,在图像文本生成里,y y y x ^ θ ( x t , t , y ) ≈ x 0 \hat{\boldsymbol{x}}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t, y\right) \approx \boldsymbol{x}_0 x ^ θ ( x t , t , y ) ≈ x 0 ϵ ^ θ ( x t , t , y ) ≈ ϵ 0 \hat{\boldsymbol{\epsilon}}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t, y\right) \approx \epsilon_0 ϵ ^ θ ( x t , t , y ) ≈ ϵ 0 s θ ( x t , t , y ) ≈ ∇ log p ( x t ∣ y ) \boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t, y\right) \approx \nabla \log p\left(\boldsymbol{x}_t | y\right) s θ ( x t , t , y ) ≈ ∇ log p ( x t ∣ y )
这种原始形式公式的一个警告是,以这种方式训练的条件扩散模型可能会学会忽略或淡化任何给定的条件信息。因此,提出了引导(guidance)作为一种更明确地控制模型赋予条件信息权重的方法,需要使用数据多样性作为代价。两种最流行的引导形式被称为分类器引导(Classifier Guidance)[10 , 20 ]和无分类器引导(Classifier-Free Guidance)[21 ]。
分类器引导
让我们从扩散模型的基于得分的方程入手,这里我们目标是学习任意噪声级别t t t ∇ log p ( x t ∣ y ) \nabla \log p(\boldsymbol{x}_t | y) ∇ log p ( x t ∣ y ) ∇ \nabla ∇ ∇ x t \nabla_{\boldsymbol{x}_t} ∇ x t
这里的log p ( y ) \log p(y) log p ( y ) x t \boldsymbol{x}_t x t
我们的最终推导结果可以解释为,学习一个无条件的得分函数和一个分类器的对抗梯度p ( y ∣ x t ) p(y|\boldsymbol{x}_t) p ( y ∣ x t ) 10 , 20 ]中,像之前推导的那样,学一个无条件扩散模型的得分同时,附带一个分类器接受任意噪声x t \boldsymbol{x}_t x t y y y
为了引入细粒度控制以鼓励或阻止模型考虑条件信息,分类器引导使用超参数项γ \gamma γ
(166) ∇ log p ( x t ∣ y ) = ∇ log p ( x t ) + γ ∇ log p ( y ∣ x t ) \nabla \log p(\boldsymbol{x}_t | y)=\nabla \log p(\boldsymbol{x}_t)+\gamma \nabla \log p(y | \boldsymbol{x}_t) \tag{166}
∇ log p ( x t ∣ y ) = ∇ log p ( x t ) + γ ∇ log p ( y ∣ x t ) ( 1 6 6 )
直觉上,当γ = 0 \gamma=0 γ = 0 γ \gamma γ
分类器引导的一个显著缺点是它依赖于单独学习的分类器。由于分类器必须处理任意噪声输入,而大多数现有的预训练分类模型都没有对此进行优化,因此它必须与扩散模型一起专门做训练。
无分类器引导
在无分类器引导[21 ]中,作者没有单独训练分类器模型,转而使用无条件扩散模型和条件扩散模型。为了推导无分类器引导的得分函数,首先重新排列公式165:
(167) ∇ log p ( y ∣ x t ) = ∇ log p ( x t ∣ y ) − ∇ log p ( x t ) \nabla \log p(y | \boldsymbol{x}_t)=\nabla \log p(\boldsymbol{x}_t | y)-\nabla \log p(\boldsymbol{x}_t) \tag{167}
∇ log p ( y ∣ x t ) = ∇ log p ( x t ∣ y ) − ∇ log p ( x t ) ( 1 6 7 )
之后,把这个替换进公式166,可以得到:
同样的,γ \gamma γ γ = 0 \gamma=0 γ = 0 γ = 1 \gamma=1 γ = 1 γ > 1 \gamma > 1 γ > 1
由于学习两个单独的扩散模型开销太大,我们可以将条件和无条件扩散模型作为一个单一的条件模型一起学习。无条件扩散模型可以通过将条件信息替换为固定的常量值(例如零),这本质上是对条件信息执行随机的dropout。无分类器引导是优雅的做法,因为只需要单一扩散模型的训练就可以更好地控制条件生成过程。
结语
概括一下我们在探索过程中的发现。首先,我们将VDM作为MHVAE的一个特例进行推导,其中有三个关键假设使得ELBO的计算易于处理和可放缩的优化。然后我们证明,优化VDM归结为学习神经网络来预测三个潜在目标中的其中一个:来自任意噪声级别的源图像、来自任意噪声图像的源噪声、或者任意噪声水平下带噪图像的得分函数。然后深入探讨了学习得分函数意味着什么,并将其与基于得分的生成模型的观点明确联系起来。最后介绍了如何使用扩散模型学习条件分布。
总之,扩散模型显示出了作为生成模型的难以置信的能力。实际上,它们为当前最先进的文本图像生成模型提供了动力,如Imagen和DALL-E 2。此外,这些模型背后的数学过程非常优雅。然而,仍有一些缺点需要考虑:
这不太可能是我们人类自然建模和生成数据的方式,我们不会用迭代去噪一个随机噪声的过程生成样本。
VDM无法产生可解释的隐信息(latents)。尽管VAE非常有希望能够通过优化其编码器来学习结构化的隐空间,但在VDM中,每个时间步长的编码器已经作为线性高斯模型给出,无法可变的优化。因此,中间的隐信息被限制为原始输入的噪音版本。
隐信息被限制与原始输入的维度相同,进一步影响了对有意义、压缩过的隐结构的学习。
采样过程开销巨大,因为必须在两种公式下运行多个去噪步骤。回想一下,其中一个限制是选择足够大的时间步T T T
最后,扩散模型的成功突出了HVAE作为生成模型的强大能力。我们已经证明,当推广到无限 的隐层次结构时,即使编码器很普通,隐维度是固定的,并且假设了马尔科夫变换,仍然能够学到强大的数据模型。这表明在一般的、深的HVAE情况下,可以进一步提高性能,这种情况下,有可能学到复杂的编码器和有语义意义的隐空间。
参考文献
[1] Diederik P Kingma and Max Welling. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.