两个图像处理问题的实例以及分析思路
这是老潘曾经做过的某个大学笔试题,代码尽可能干净简练并且能够快速解决问题,比较值得记录并且研究。尤其是第二题,在方法的设计上,对于结果的约束需要一些技巧才行,无脑用绝对误差很难行得通。
这些题目没有标准答案和做法,这里只是抛砖引玉,欢迎进一步交流优化改进。
下面是题目和解决思路以及配套完整代码(链接:https://github.com/divertingPan/utility_room/blob/master/task_2022.ipynb)。
第一题
题目:构建一个自编码器,至少包含4个编码层。编码一个至少有500副自然图像的灰度图片,分辨率为600x600
其实这一个做法和很久之前的一篇文章基本一样(复习Pytorch的使用方法,在套路的基础上灵活应变),只不过这里的图像编解码前后,分辨率都比较大(要600x600)。所以在模型的选择上可能要做一些巧妙的处理。我选择使用了Unet结构的模型,虽说这样能够解出题目,但转念一想,这样做的话,如果想要取出编码之后的隐向量,单使用这个编码去还原图像就不太可行。因为在解码器解码过程中需要依赖中间同级的编码层信息。当然也可以把这几个中间层互传的信息也看做隐向量去处理。
做这个用的数据集我拿的是DIV2K,但是这个数据量实际上不大,做做toy example可以,想实用的话还是搞点大的数据集吧。
第二题
题目:从CIFAR10中取出1000副图像,之后给定一个图像对和,构建一个网络模型能够以他们的平均作为输入,输出两个原始的图像
最开始用的MAE当损失函数,但是这样是有一点违反直觉的,因为不一定要限制左边分叉只能输出和第一个图接近的结果。换句话说就是,和输入网络之后,输出可以是,也可以是。所以说MAE没法做到这种能够交换顺序的衡量。并且,真的试了一下实验结果也不好:
这里img_1和img_2是两个输入,img_merge是融合的图像,pred_1和pred_2是两个预测结果。可以看到,模型仿佛在摆烂,只要我仍然输出均值图像,那这个输出就离两个目标都不算太远。其实这样想一下也是有原因的:如果求平均图像的真实来源,可能是或者,结果对于同样的,模型一会儿要预测成一会要,这自然是两个相反的方向,模型摆烂的确是趋于中庸的自然结果。
后来仔细思考了一下,决定施加一些专门的约束。
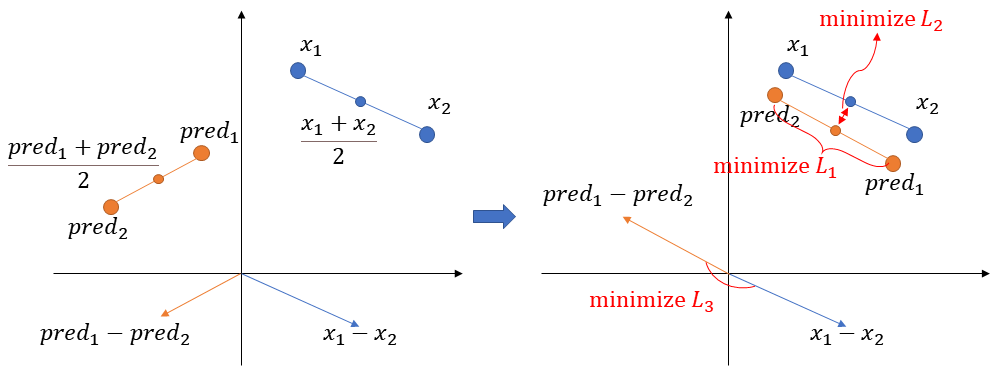
首先,顺承上面模型摆烂时候发生的情况,一对预测结果的大致位置至少要和真实情况的大致位置相差不大。也就是说,两个输出结果的均值,应该和两个真实图像的均值尽量一样。
反应在图上就是让两个中心点尽量靠近,让pred预测的中心点尽量接近实际的真值。用式子表达的话,可以写成
就是两个输出的均值,和两个真实值的均值,看均值之间的距离。
第二,进一步,这个位置确定了,但是两个结果之间会有一定的距离,可以想作是,以上面说的那个均值点为中心,各自向两端的距离。这个距离,对于预测和真值也应该是一致的。
反应在图上就是让实线括号所指的距离,尽量接近虚线括号所指的距离。式子表达是
意思是,两个预测之间的距离,以及两个真实图之间的距离,看这两个距离之间差别多大,只关心绝对值不看正负号。
这时候很自然的会发现,两个样本点在空间上会有一个夹角。对于我们希望的情况应该是,这两个样本点连成的线应该平行。这样刚好对应了两个输出顺序可以不严格一致的情况。
反应在图上就是让两条线之间最小的夹角尽量小。这个可以用余弦相似度衡量,余弦相似度取值在之间,两个向量同向平行是1,反向平行是-1,越垂直越趋向于0。从图上也可以看出来,具体的样本顺序是无所谓的,正好也符合前面所说过的。所以可以这样做损失函数
两个样本做差是求出他们之间连线的方向向量。取了余弦相似度的绝对值就是只看平行度,不看方向。用1做减是为了反向他,相当于最小这个式子的时候就是最大化余弦相似度。
这样就可以写代码了,损失函数loss就写成下面这种
loss_func = nn.L1Loss()
parallelism = torch.mean(1 - torch.abs(F.cosine_similarity((img_1-img_2).view(-1, 3*32*32), (pred_1-pred_2).view(-1, 3*32*32), dim=1)))
loss = torch.abs(loss_func(img_1, img_2) - loss_func(pred_1, pred_2)) + loss_func(0.5 * (pred_1 + pred_2), 0.5 * (img_1 + img_2)) + parallelism
在同样的训练次数下,模型显然有了更好的表现: