硬币系列三 | 硬币自动分类的一个论文复现
MATLAB代码地址:https://github.com/divertingPan/coin_machine/tree/master/RFR_GM
书接上回,经过自动检测和裁剪之后,已经有很多切割整齐的硬币照片了,再来看看相似检测的方法。
一开始的思路也是极其简单,既然前面做了边缘提取,而对于硬币的种类,人眼最关心的也是和轮廓、花纹相关的信息。那就利用边缘信息来检测,怎么检测呢?
拿待检测的图的边缘,和所有标准图的边缘一个一个叠起来比较,和谁重合的面积越大,就和谁最像。虽然这个思路简单到小学二年级的同学都会笑出声,但这个方法在使用得当的时候,准确率可以高达40%(不行还是太弱了)
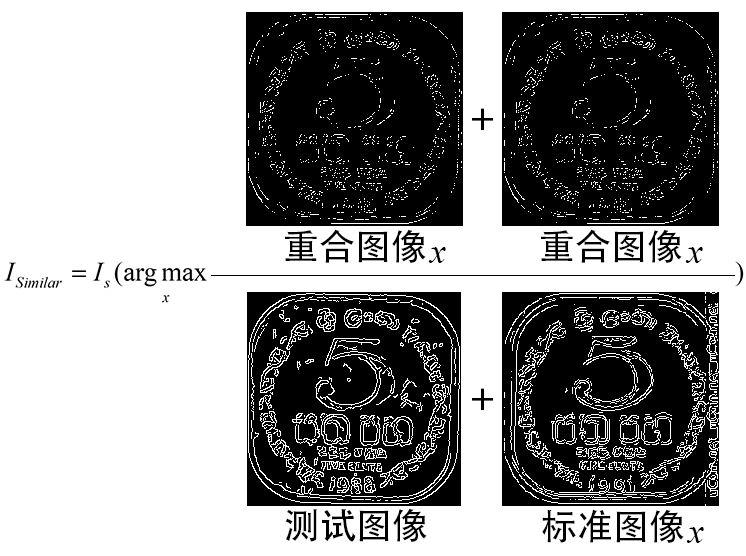
设待检测的图像的边缘信息为,个标准图像的边缘信息为,这里要求和图像尺寸均一致。这样,与待测图像最接近的标准图像为
说人话:就是看看标准图和测试图重合区域的面积,哪个面积越接近测试图像的面积,就是最相像的标准图像(为了防止混乱,这里强调一下,“面积”指的是图片里白色区域的面积,或者说白色像素块的数量。这里涉及的图都是只有黑色和白色两个颜色的)。

老潘用手工方式标注了200个硬币配对,在这上面做点简单测试,这种方法准确率只有8%,经过观察大部分硬币图片都被识别成了这两个

这时候我有一个猜测,如果某个标准图像非常极端的全部为白色,那么待测图像和标准图像的重合范围肯定是非常大的(重合范围就是100%的待测图像),所以上面的方法需要改一下。必须同时考虑测试图和标准图。这里将的判别方法改写为
说人话,就是看看标准图测试图重合面积、测试图面积以及标准图的面积情况,只有同时和两者都接近的才能被选作相似的图片配对。
这个方法的准确率迅猛提升到了40%,但是该方法有一个致命的bug,就是一旦硬币的角度稍有旋转(实际这个情况却很容易发生),识别率显然会受到影响。而且数据量增大也会使准确率和速度逐渐降低。速度降低很显然,至于准确率下降,老潘在测试的时候确实发现有这个现象,如果想想为什么这样,个人猜测一个可能的解释应该是:数据分布的空间有限(和图片的尺寸有关,固定大小的图片,像素点取值是有限种可能的情况,而且我们用边缘信息,图中像素点只取0-1)。数据少的时候,数据分布更可能散的比较远,中间的空隙会很大(相当于画一个圈,大一些小一些歪一些都能把目标点套住),而数据越来越多就会让各个数据更拥挤,每个数据点之间的距离缩小了,这个时候随便画个圈就不是那么容易套住想要的东西了,很有可能套到别的点上。而这个小学二年级方法显然不能如此精准地在拥挤的点中选择目标,所以准确率会下降。(如果有大佬能给出规范的解释老潘给你投币三连)
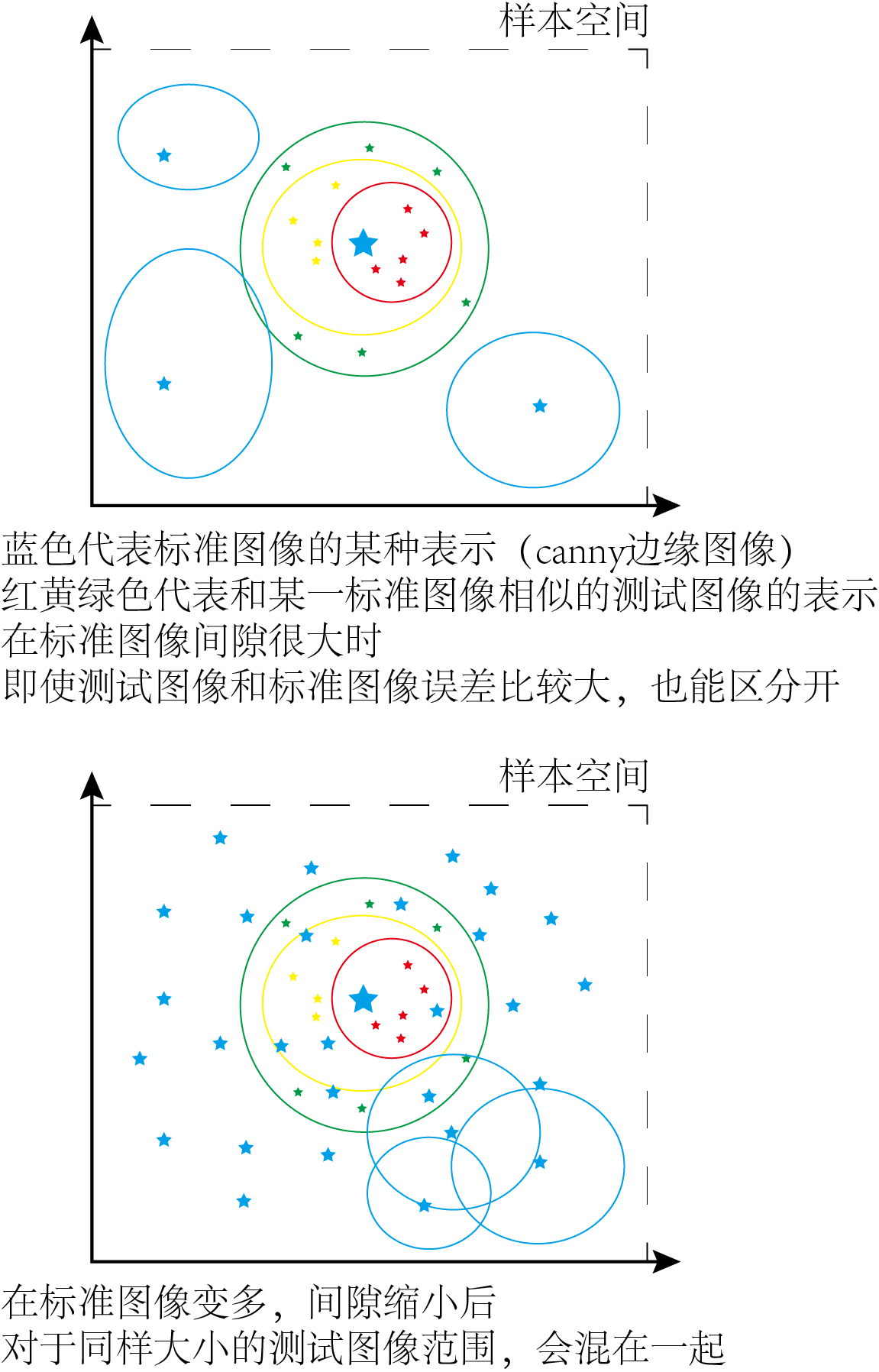
所以有没有哪种方法可以在旋转或者光照发生变化时,对同一个硬币图案的描述比较稳定,对不同硬币的描述差别较大呢?显然这马上使我们想到了使用LBP方法来尝试。LBP(Local Binary Patterns)可以看做一类方法的统称。大致思想就是在图中选一个区域,把这个区域的变化情况用数字分类表达。这里老潘找到一个专门针对硬币分类的LBP思想方法的论文《Image-based coin recognition using rotation-invariant region binary patterns based on gradient magnitudes》[1]。论文思路十分简单,这里进行简单的分析与复现。
算法本身并不困难,总体思路如图
首先把硬币图片切割好(这我们早已做好了),然后求硬币的梯度图Gradient Magnitudes(公式2),之后用蜘蛛网状分区,分几个环和几个扇(取值多少属于调参时要考虑的,呼唤调参侠),对每个小块里的值,都有特别的计算方法(一个是求区域里的均值,一个是公式4),再变换到intra RBP和inter RBP(公式6和7)。看每一个环,他的各个扇区一圈就代表了一个二值模式,上面的圆有3圈,所以有3个二值模式,下面的圆同理。
对于每个二值模式编码编成多少?在同一个作者的《Rotation and flipping robust region binary patterns for video copy detection》[2]里介绍了。对于所有可以通过翻转和旋转重合的模式,就算为一组,如图
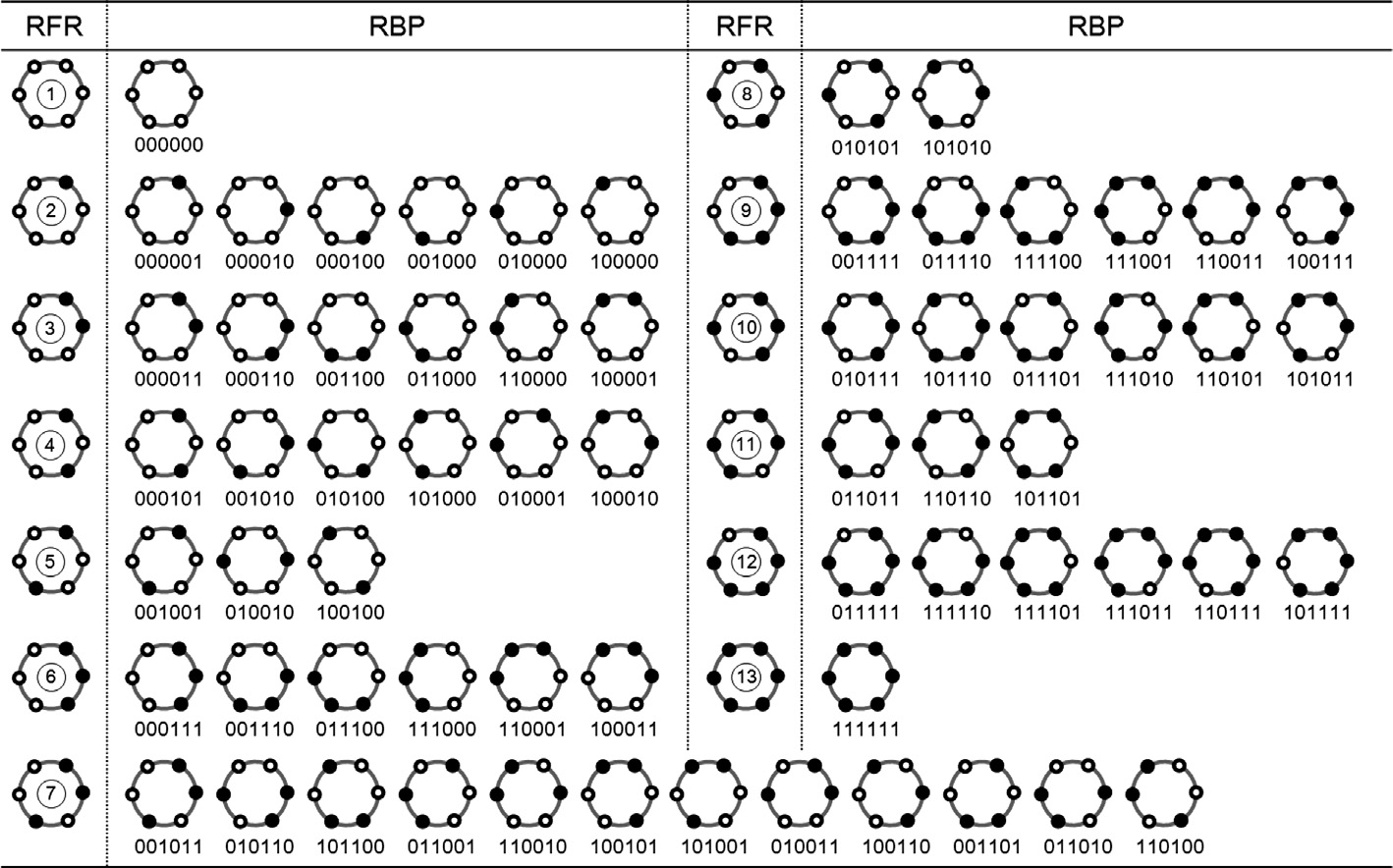
比如说RFR是②的那一排,一圈上只有一个黑点的,都是一样的模式(可以旋转和翻转互相重合)所以作为一组。这里面的组顺序没什么特别要求,只要相同模式归为一组并且编个号就行。
另外对于评判两类模式之间的距离,作者用的方法是,计算两个组之间每组所有模式两两的汉明距离(Hamming Distance),取最小的为两类之间距离。
思路已经捋清楚了,我们甚至可以当堂完成这个作业。这一次老潘用了MATLAB,没有用python(不知道为什么涉及到这种纯图像的问题我更习惯先打开MATLAB)。写程序很快,一晚上就可以写完甚至不需要熬夜,但是优化这个东西却耗了老潘一下午。
先来简单的。第一步求图像的梯度图像,太简单了不解释。(我突然觉得这里也可以优化的)
M = zeros(I_size - 2);
for x = 2:I_size - 1
for y = 2:I_size - 1
M(x-1, y-1) = sqrt((I(x+1, y) - I(x-1, y))^2 + (I(x, y+1) - I(x, y-1))^2);
end
end
然后做图像的扇区,求出每个扇区下的平均值。这里稍稍有点绕,我选择先计算环,再计算角度,再取交集,就像下图所示。

r = (I_size - 2) / 2;
center_point = r;
axis_x = zeros(I_size - 2);
for row = 1:I_size - 2
axis_x(row,:) = [1:I_size - 2];
end
axis_y = zeros(I_size - 2);
for column = 1:I_size - 2
axis_y(:,column) = [1:I_size - 2];
end
condition_r = abs(sqrt((axis_x-center_point).^2 + (axis_y-center_point).^2));
condition_angle = atan2(axis_y-center_point, axis_x-center_point)/pi*180+180;
for ring = 1:rings
for region = 1:sub_regions
area_r = condition_r < ring*(r/rings) & condition_r >= (ring-1)*(r/rings);
area_angle = condition_angle < region*(360/sub_regions) & condition_angle >= (region-1)*(360/sub_regions);
插个嘴做一些解释:这里的area_r和area_angle相当于蒙版,我们只要直接和图片点乘就可以选出要的区域(1乘一个数还是这个数,0乘一个数一直是0)
取两个蒙版的交集也是同理,直接互相点乘即可,得到的矩阵就是交集area_need。
注释掉的地方可以生成一个动态的GIF图片,展示了每圈每个扇区下的梯度图像情况。
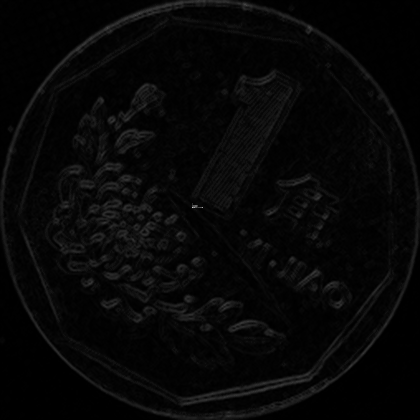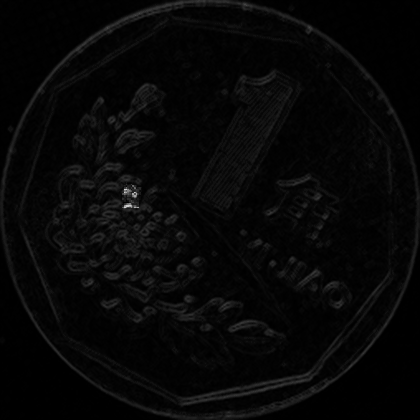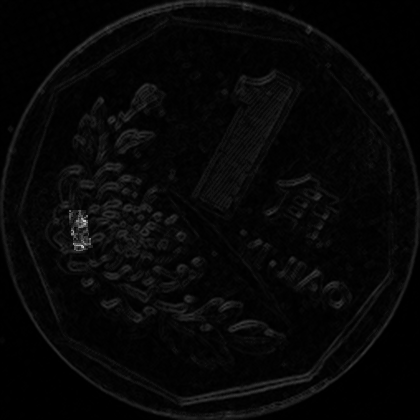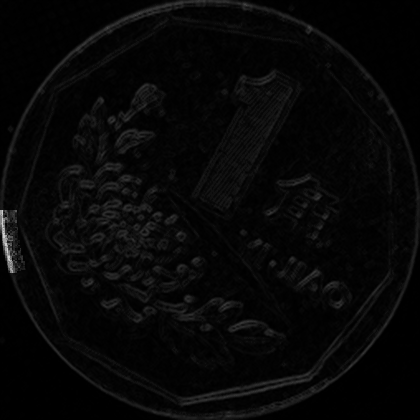
之后计算每个区域下的均值,存下来即可。
area_need = area_r .* area_angle;
area_gradient = M .* area_need;
% % save a gif to observe
% imshow(area_gradient, [], 'border','tight', 'initialmagnification','fit');
% F=getframe(gcf);
% I=frame2im(F);
% [I,map]=rgb2ind(I,256);
% if pic_num == 1
% imwrite(I,map,'RFR_log/area.gif','gif', 'Loopcount',inf,'DelayTime',0.1);
% else
% imwrite(I,map,'RFR_log/area.gif','gif','WriteMode','append','DelayTime',0.1);
% end
% pic_num = pic_num + 1;
m(ring, region) = sum(area_gradient(:)) / sum(area_need(:));
end
end
之后的公式3至7的计算略,没什么好解释的。贴出来也只会令人头晕。
好了,就差构造一个查找表IND和一个距离矩阵了,但是具体做的时候就没那么简单了。
1
先说构造IND,这个表用来把一个010101这样的模式换成他所在类的号码。因为组比较多,所以用一次算一次比较慢,不如用空间换时间。于是第一天晚上挂机一宿,发现这个表还没罗列好。遂优化。一开始的想法是用一个表格当做查找表,行数就是类别号,每行存储这类的二值模式0101码。但是问题一,表里会有很多冗余数据,比如全0的这类,由于数组尺寸必须一样,需要把后面空缺的都填满。就存了20个全0的模式。问题二,时间很慢而且会越来越慢。因为每一个模式都要去表里查找是否出现过,表越大查的越慢。
于是想了一招,采用Map格式存储,首先要声明一下变量
IND = containers.Map;
代表我们要用Map存储IND表格,之后,为了提高查找效率,不用类号做索引,用二值模式做索引,这样一来可以很快查到表里有没有出现过这个二值模式,二来在使用的时候,把图的二值模式转成类别号也会快。这时候遍历所有的二值模式,对于这一组二值模式,如果有一个没在之前出现过,那就把这一组全存下,并且给一个统一的组号(这一组是用某一个二值模式经过循环移位和翻转出来的)。如果在之前出现过,就代表这一组的二值模式都已经在这个表里有过了(通过旋转和移位终究会变成一样的)。判断和存储的方法为
if ~isKey(IND, dec2bin(CP_FP_dec(1), sub_regions))
for index_map = 1:length
IND(dec2bin(CP_FP_dec(index_map), sub_regions)) = ind;
end
ind = ind + 1;
end
(只记录了判断键值是否出现过,整体代码见GitHub)
于是一宿未完的问题,10分钟就可以解决了。其中5分钟用来把数据保存到磁盘上用来下次直接查找该换固态硬盘了。
2
下一个问题是计算两类之间的距离,原论文仍然是做了一个矩阵,可以直接在里面查两类的距离,但是我做的时候发现这个矩阵太大,内存会爆(计算一下这个矩阵只占729Mb,MATLAB居然放不下)。咱也不知道作者用了什么黑科技(也许是转了C语言),我想了想,干脆在判断图片的时候直接计算,也差不了多长时间。
还是挺占时间的,实际用的时候发现只判断两个图片就要将近半分钟。这要是再一个一个比对过去,天荒地老。遂优化。最开始就是粗暴的两个for循环,然后一个一个的取两个类别号,然后计算。发现不行,有点慢,于是改用矩阵计算。先做两个类别号(其实是两组,一个图片会有一组类别号)的排列组合矩阵
% reference: https://www.ilovematlab.cn/thread-321138-1-1.html
[m, n] = meshgrid(RFR_i_list_dec, RFR_j_list_dec');
[res(:,1), res(:,2)] = deal(reshape(m, [], 1), reshape(n, [], 1));
然后计算这个矩阵按行的汉明距离,取这个矩阵的min就是两个类的距离。
DH = dec2bin(bitxor(res(:,1), res(:,2)));
[length, ~] = size(DH);
DH2 = uint8(zeros(length, 1));
for i = 1:length
DH2(i) = sum(DH(i,:)=='1');
end
min_Hamming = min(DH2);
之后发现还是很占时间,偶然瞥到,在每一轮循环里都有这么个操作
key = keys(IND);
value = uint32(cell2mat(values(IND)));
把类号和二值模式从Map格式里面拿出来,这个拿的动作很耗时。所以就一开始取出,直接作为参数传给后面的一系列函数。原本两个图片对比时间要大概半分钟,现在只需半秒。速度提升了60倍。
不过速度还是比较慢,不知道那个在线识别硬币的网站用的到底是什么方法。如果选择做出来距离对照表的话,拿空间换时间,应该速度就会很快了。但是我估算目前的小需求下,做查找表的时间和直接做计算的时间,好像做表不是太划算。
话说回来,用这个方法的检测准确率可以达到45.5%,远不及论文中所达到的准确率(89.1%)。我使用了和作者一致的参数,但是数据集不一样。作者使用的是远古版本的MUSCLE-CIS数据集,这是在2006年办的一个硬币识别比赛用的数据集,原链接已经失效,在网上也很难搜索到相关的数据,只有在偶尔一些论文里有零星展示,在论文[3]里给了两个数据集内的图片。
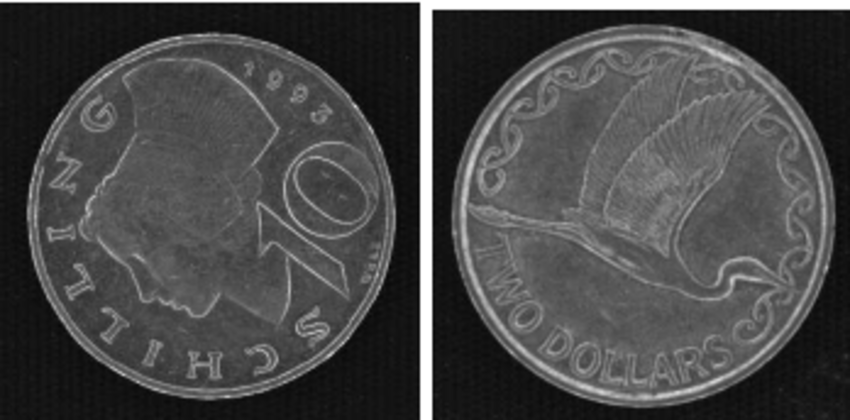
可以看到这个图像和直接用手机拍的画面差别挺大的,这个边缘非常清晰,有可能是用了特殊的光源和相机拍摄的。在这种优良干净的数据上,我相信小学生方法也能有不错的效果。但是在具体生活场景上,如何在光照不佳,数据量小的情况下提高检测效率,还是一个有待研究的问题。
经过简单的进一步调研,在文章[4]中提到,MUSCLE-CIS分辨率低并且经过了很强的预处理,实际场景很难得到这样的图片。但是硬币数据集还有很多,例如文章中给出的这个例子,可以看到实际生活中主要面对的还是后面这几类图像。这个文章着眼于提取硬币表面的文字,更深刻的分析了硬币识别里面的各种技术问题,而且作者他们也自己建立了一个数据集。论文在线网址:
https://www.frontiersin.org/articles/10.3389/fict.2017.00009/full
(这个作者也研究过硬币分类的问题,用的貌似是类似SIFT那种方法,看起来好像很吊的样子,这篇文章[5]的方法作为作业下节课找同学上台讲解)
这次老潘用的自建数据集也会放在GitHub上,想研究的同学可以拿去玩一玩:https://github.com/divertingPan/coin_machine/tree/master/dataset
参考文献:
[1] Kim S, Lee S H, Ro Y M, et al. Image-based coin recognition using rotation-invariant region binary patterns based on gradient magnitudes[J]. Journal of Visual Communication and Image Representation, 2015: 217-223.
[2] Kim S, Lee S H, Ro Y M, et al. Rotation and flipping robust region binary patterns for video copy detection[J]. Journal of Visual Communication and Image Representation, 2014, 25(2): 373-383.
[3] Zaharieva M, Hubermoerk R, Noelle M, et al. On ancient coin classification[C]. ieee virtual reality conference, 2007: 55-62.
[4] Pan X, Tougne L. A New Database of Digits Extracted from Coins with Hard-to-Segment Foreground for Optical Character Recognition Evaluation[J]. Frontiers in ICT, 2017.
[5] Pan X, Puritat K, Tougne L, et al. A New Coin Segmentation and Graph-Based Identification Method for Numismatic Application[C]. international symposium on visual computing, 2014: 185-195.